
1. 写出下列直线的点斜式方程:
(1)经过点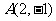 ,斜率为
,斜率为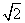 ;
;
(2)经过点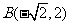 ,倾斜角为
,倾斜角为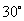 ;
;
(3)经过点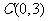 ,倾斜角是
,倾斜角是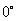 ;
;
(4)经过点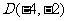 ,倾斜角是
,倾斜角是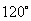 .
.
3.方程 叫做直线的斜截式方程,其中 叫做直线在 上的截距.
[精典范例]
例1:已知一条直线经过点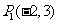 ,斜率为
,斜率为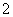 ,求这条直线的方程.
,求这条直线的方程.
[解]
 例2:直线
例2:直线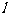 斜率为
斜率为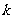 ,与
,与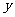 轴的交点是
轴的交点是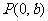 ,求直线
,求直线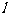 的方程.
的方程.
[解]
例3:(1)求直线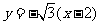 的倾斜角;
的倾斜角;
(2)求直线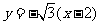 绕点
绕点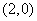 按顺时针方向旋转
按顺时针方向旋转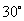 所得的直线方程.
所得的直线方程.
[解]
例4:在同一坐标作出下列两组直线 ,分别说出这两组直线有什么共同特征?
(1)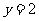 ,
,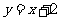 ,
,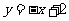 ,
,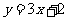 ,
,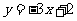 ;
;
(2)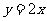 ,
,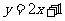 ,
,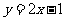 ,
,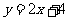 ,
,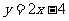
[解]
[选修延伸]
例5:等腰三角形ABC的顶点为A(-1,2),又AC的斜率为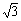 ,点B(-3,2),求直线AC,BC及<A的平分线所在直线的方程.
,点B(-3,2),求直线AC,BC及<A的平分线所在直线的方程.
追踪训练
2.直线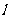 经过点
经过点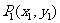 ,当直线斜率不存在时,直线方程为
;当斜率为
,当直线斜率不存在时,直线方程为
;当斜率为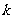 时,直线方程为
,该方程叫做直线的点斜式方程.
时,直线方程为
,该方程叫做直线的点斜式方程.
1.求直线的方程,其实就是研究直线上任意一点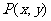 的
之间的关系.
的
之间的关系.
3.掌握斜率不存在时的直线方程,即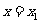 .
自学评价
.
自学评价
2.能通过待定系数(直线上的一个点的坐标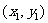 及斜率
及斜率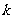 ,或者直线的斜率
,或者直线的斜率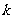 及在
及在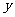 轴上的截距
轴上的截距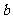 )求直线方程;
)求直线方程;
1.掌握由一点和斜率导出直线方程的方法,掌握直线的点斜式方程;了解直线方程的斜截式是点斜式的特例;
2.设点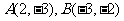 ,直线
,直线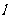 过点
过点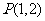 ,且与线段
,且与线段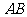 相交,求直线
相交,求直线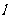 的斜率的取值范围.
的斜率的取值范围.
例5: 若过原点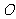 的直线
的直线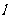 与连结
与连结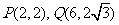 的线段相交,求直线
的线段相交,求直线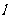 的倾斜角和斜率的取值范围.
的倾斜角和斜率的取值范围.
分析:结合图形可知(图略),直线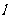 介于直线
介于直线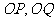 之间,即可得倾斜角范围;再根据倾斜角变化时,斜率变化规律可得斜率范围.
之间,即可得倾斜角范围;再根据倾斜角变化时,斜率变化规律可得斜率范围.
追踪训练二
1.已知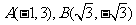 ,则直线
,则直线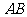 的倾斜角
的倾斜角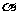 和斜率
和斜率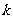 分别为( )
分别为( )
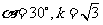
|
学生质疑 |
|
|
教师释疑 |
|
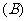
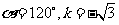
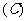
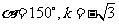
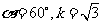
4、设点A(-1,1),B(x,2),C(-2,y)为直线l上三点,已知直线的 斜率k=2,则x= .
|
学生质疑 |
|
|
教师释疑 |
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com