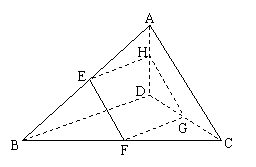
6.如图, E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点, 求证:

　 (1)四点E、F、G、H共面;

　 (2)BD//平面EFGH , AC//平面EFGH .

拓展延伸

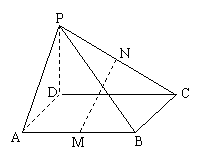
如图, 在四棱锥P-ABCD中, M、N分别是AB、PC的中点, 若ABCD是平行四边形, 求证: MN//平面PAD .

节学习疑点：

5.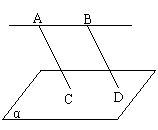如图, AB//α, AC//BD , C∈α, D∈α, 求证: AC=BD.

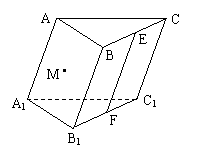
4.如图, 在三棱柱ABC-A₁B₁C₁中, E∈BC , F∈B₁C₁ , EF//C₁C , 点M∈平面AA₁B₁B , 点M、E、F确定平面γ, 试作平面γ与三棱柱ABC-A₁B₁C₁表面的交线, 其画法____________________________________________________________________________

　 ___________________________________ .

3.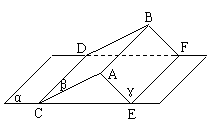如图α∩β=CD , α∩γ=EF , β∩γ=AB , 若AB//α, 则CD与EF___________(“平行”或“不平行”.

2.梯形ABCD中, AB//CD, AB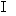α, CD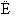α, 则CD与平面α内的直线的位置关系只能是(　 )

　 A.平行　　　 B.平行或异面　　

C.平行或相交 D.异面或相交　　　　

1.给出下列四个命题

　 ①若一条直线与一个平面内的一条直线平行, 则这条直线与这个平面平行;

②若一条直线与一个平面内的两条直线平行, 则这条直线与这个平面平行;

③若平面外的一条直线和这个平面内的一条直线平行, 那么这条直线和这个平面平行;

④若两条平行直线中的一条与一个平面平行, 则另一条也与这个平面平行.

其中正确命题的个数是　　　　　 (　　 )　　　　　　　　　　　　　　　　　　　　　　　　

A. 0　　 B. 1　 　　　C. 2　　　　 D. 3

24．(06江苏高考)

在正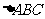中，E、F、P分别是AB、AC、BC边上的点，满足AE：EB=CF：FA=CP：PB=1：2(如图1)，将△AEF沿EF折起到△A₁EF的位置，使二面角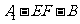成直二面角，连结A₁B、A₁P(如图2)

⑴求证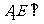：平面BEP；

⑵求直线A₁E与平面A₁BP所成角的大小；

⑶求二面角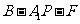的大小(用反三角函数值表示)。

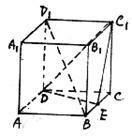
23．在正方体AC₁中，E为BC中点(1)求证：BD₁∥平面C₁DE；

(2)在棱CC₁上求一点P，使平面A₁B₁P⊥平面C₁DE；

(3)求二面角B-C₁D-E的余弦值.

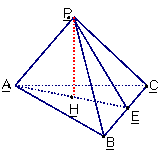
22.在三棱锥P-ABC中，三条侧棱PA，PB，PC两两垂直，H是△ABC的垂心，求证：

⑴PH^底面ABC 　⑵△ABC是锐角三角形.

21.圆锥的底面半径为5cm , 高为12cm , 当它的内接圆柱的底面半径为何值时, 圆锥的内接圆柱全面积有最大值; 最大值是多少?