3．画法：平面衬托法(举例说明)

2．异面直线的特点　　　　　　　　　　　　 　　　　　　　

1.　　 异面直线的概念　　　　　　　　　　

知识网络

学习要求

1. 掌握异面直线的定义．

2理解并掌握异面直线判定方法．

.3.掌握异面直线所成的角的计算方法．

自学评价

3．如图，已知AA′，BB′，CC′，不共面，且AA′//BB′,AA′=BB′,

BB′//CC′, BB′=CC′.

求证：△ABC≌△A′B′C′

A′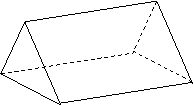

A

B′

B　　　　　　　　　　　　　　 C′

C

思维点拔：

凡“有且只有”的证明，丢掉“有”

即存在性步骤，或丢掉“只有”即唯一性的证明都会导致错误发生，即证明不全面，思维不严谨所致。

求证：过直线外一点有且只有一条直线和这条直线平行．

已知：

求证

总结：(1)凡上述两类问题型的证明应有两步，即先证明事实存在，再证明它是唯一的(2)解答文字命题必须将文字语言“译”成符号语言，然后写出“已知和求证”需要作图时，要把图形作出来，最后给出“解答(证明)”

2.若OA//O₁A₁ , OB//O₁B₁ , 则∠AOB与∠A₁O₁B₁关系　　　(　)　　　　　　　　　　　　

　 A.相等　　 　　　 B.互补　　　　　

C.相等或互补　　 D.以上答案都不对

1. 设AA₁是正方体的一条棱，这个正方体中与AA₁平行的棱共有　(　)

A.1条　　　　B.2条

C.3条　　　　D.4条

3．等角定理：　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　 [精典范例]

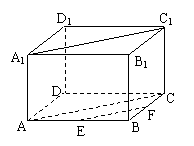例1：.如图, 在长方体ABCD-A₁B₁C₁D₁中, 已知E、F分别是AB、BC的中点, 求证: EF//A₁C₁

思维点拔：

证两直线平行的方法：

(1)利用初中所学的知识

　　(2)利用平行公理．

追踪训练1

已知：棱长为a的正方体ABCD-A₁B₁C₁D₁中，M,N分别为CD,AD的中点，求证：四边形MNAC是梯形．

　　　　N

点评：要证梯形，必须证明有两边平行且相等，平行的证明要善于联想平面几何知识．

例2：如图. 已知E、E₁分别为正方体ABCD-A₁B₁C₁D₁的棱AD、A₁D₁的中点, 求证: ∠C₁E₁B₁=∠CEB .

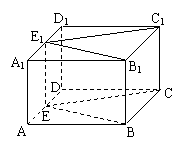
分析：设法证明E₁C₁//EC,E₁B_1//EB

证明：

等角定理：如果一个角的两边和另一个角的两边分别平行并且方向相同，那么这两个角相等。

等角定理的证明

　已知: ∠BAC和∠B₁A₁C₁的边AB//A₁B₁ , AC//A₁C₁ , 并且方向相同.

求证: ∠BAC=∠B₁A₁C₁

追踪训练2

2.　　 公里4：　　　　　　　　　　　　　

符号表示： 　　　　　　　　　　　　　　　　　　　

思考：经过直线外一点，有几条直线和这条直线平行

答：

1.　　 空间两直线的位置关系

位置关系　共面情况　公共点个数

相交直线

平行直线

异面直线