
3.棱台的定义:
表示法:
思考:棱台的特点:.
[答]
2. 棱锥的定义:
表示法:
思考:棱锥的特点:.
[答]
1. 棱柱的定义:
表示法:
思考:棱柱的特点:.
[答]
4.了解多面体的概念和分类.
[课堂互动]
自学评价
3.了解棱柱、棱锥、棱台这几种几何体简单作图方法
2.了解棱柱、棱锥、棱台中一些常用名称的含义。
重点:空间直线,平面的位置关系。柱、锥、台、球的表面积和体积的计算公式。平行、垂直的定义,判定和性质。
难点:柱、锥、台、球的结构特征的概括。文字语言,图形语言和符号语言的转化。平行,垂直判定与性质定理证明与应用。
第一课时 棱柱、棱锥、棱台
[学习导航]
|


 学习要求
学习要求
1.初步理解棱柱、棱锥、棱台的概念。掌握它们的形成特点。
2.正方体, 等边圆柱(底面直径和高相等的圆柱), 球的体积相等, 则哪一个表面积最小?
思路:设三种几何体的体积为V.
则正方体棱长a=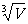
所以正方体的表面积=6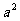 =
=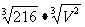
等边圆柱的底面半径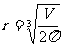 .
.
等边圆柱的表面积=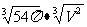
球半径R=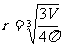
球的表面积=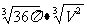
所以:
正方体的表面积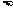 等边圆柱的表面积
等边圆柱的表面积 球的表面积.
球的表面积.
1. P、A、B、C为球面上的四个点, 若PA、PB、PC两两互相垂直, 且PA=3cm 、PB=4cm、PC=6cm , 求这个球的表面积.
答案:球半径R=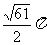
所以球的表面积为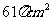
|
学生质疑 |
|
|
教师释疑 |
|
2.会求一些球的组合体中的面积与体积的问题.
[课堂互动]
自学评价
球的表面积公式: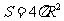 .
.
[精典范例]
例1:已知一个正四面体内接在一个表面积为36π的球内, 求这个四面体的表面积和体积.
[解]
设球半径为R,正四面体棱长为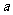 .
.
则R=3,且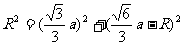
得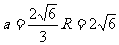
所以表面积=4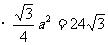
体积=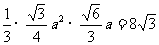 .
.
注:棱长为a的正四面体的外接球的半径R=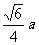 ,内切球的半径r=
,内切球的半径r=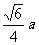 .
.
例2:已知上、下底半径分别为r、R的圆台有一内切球,
(1) 求这圆台的侧面积S1 ;
(2) 求这圆台的体积V .
(3) 求球的表面积与体积.
[解]
(1) S1=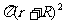
(2)由于圆台高
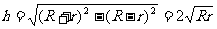
所以体积=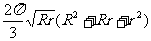
(3)球的表面积=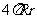
球的体积=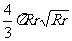 .
.
 思维点拨
思维点拨
一些重要结论要是能记住那将是非常好的事情.如正四面体外接球半径、内切球半径与正四面体棱长的关系式。
追踪训练
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com