
3.求证: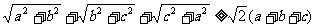
证: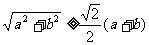
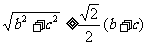
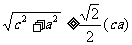
三式相加化简即得
补充:1.已知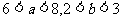 ,分别求
,分别求 的范围
的范围
(8,11) (3,6) (2,4)
2.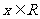 试比较
试比较 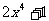 与
与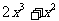 (作差
(作差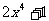 >
>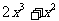 )
)
基本不等式(即平均不等式)
证:∵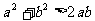
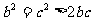
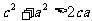
以上三式相加: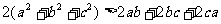
∴
4.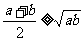 的几何解释:
的几何解释:
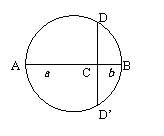 以
以 为直径作圆,在直径AB上取一点C,
过C作弦DD’^AB 则
为直径作圆,在直径AB上取一点C,
过C作弦DD’^AB 则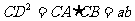
从而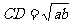
而半径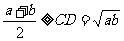
3.基本不等式: 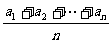 ≥
≥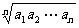
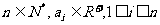
这个结论最终可用数学归纳法,二项式定理证明(这里从略)
语言表述:n个正数的算术平均数不小于它们的几何平均数。
2.点题:算术平均数与几何平均数
1.如果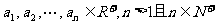 则:
则:
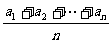 叫做这n个正数的算术平均数
叫做这n个正数的算术平均数
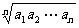 叫做这n个正数的几何平均数
叫做这n个正数的几何平均数
定理:如果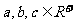 ,那么
,那么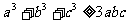
(当且仅当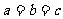 时取“=”)
时取“=”)
证明:∵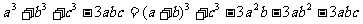
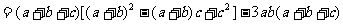
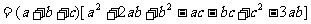
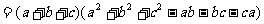
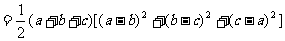
∵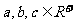 ∴上式≥0 从而
∴上式≥0 从而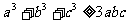
指出:这里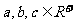 ∵
∵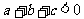 就不能保证
就不能保证
推论:如果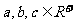 ,那么
,那么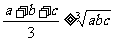
(当且仅当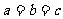 时取“=”)
时取“=”)
证明: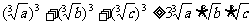

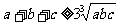

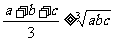
证明:∵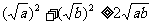 ∴
∴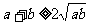
即: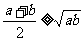 当且仅当
当且仅当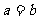 时
时 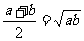
注意:1.这个定理适用的范围: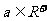
2.语言表述:两个正数的算术平均数不小于它们的几何平均数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com