
20.(1)AB=acos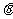 ,AC=asin
,AC=asin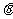 ∴S1=
∴S1=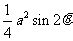 设PQ=x
设PQ=x
则AP=xcos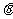 ,BP=(a
,BP=(a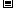 x)cos
x)cos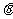 Rt△BPQ中 (a
Rt△BPQ中 (a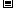 x)cos
x)cos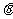 sin
sin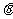 =x
=x
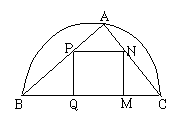 ∴x=
∴x=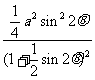
(2)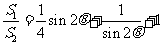
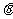 ∈(0,
∈(0,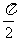 )
)
令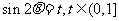
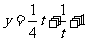 在(0,1]↓
在(0,1]↓
∴t=1时,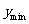 =
=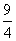 ,此时
,此时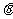 =
=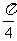 ∴
∴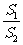 最小值为
最小值为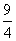
19.解:(1)f/(x)=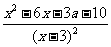
f/(1)=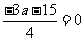 ∴a=
∴a=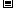 5
5
令f/(x)=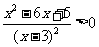
∴x<1或x>5
∴f(x)的增区间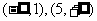 ;减区间(1,3),(3,5)
;减区间(1,3),(3,5)
(2)B={y|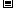 4≤y≤
4≤y≤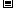 3}
3}
g/(x)=3x2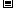 3>0
3>0 x<
x<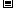 1或x>1
1或x>1
∴g(x)在[0,1]↓,[1,2]↑
∴A={y|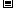 m2+4m
m2+4m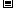 2≤y≤
2≤y≤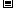 m2+4m+2}
m2+4m+2}
又B≤A
∴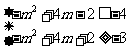 解得
解得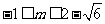 或
或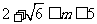
18.(1)f(x)=sin(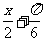 )+1
)+1
T=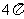
对称中心(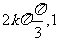 )
)
(2)(2sinA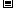 sinC)cosB=sinBcosC
sinC)cosB=sinBcosC
2sinBcosB=sin(B+C)=sinA
2sinA>0
∴cosB=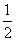
又0<B<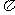
∴B=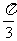
所以,f(B)=sin(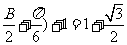 。
。
15. 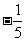 16.
16. 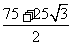 17.
17. 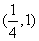
11. 1 12. 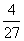 13.
13. 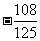 14. 1
14. 1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
C |
A |
A |
B |
C |
C |
B |
C |
D |
C |
22.(满分15分)定义在(0, )的函数f(x)的导函数记为f/(x),已知
)的函数f(x)的导函数记为f/(x),已知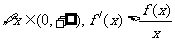 .http://www.
.http://www.
(1)设F(x)=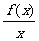 ,判断F(x)的单调性;
,判断F(x)的单调性;
(2)设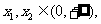 比较
比较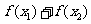 与
与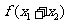 大小,说明你的理由.
大小,说明你的理由.
2009年金华一中高三9月月考(文)答案
21.(满分15分)定义在R上的函数f(x)=ax3+bx2+cx+d满足:函数f(x)的图象关于原点对称;函数f(x)的图象过点(3,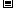 6);函数f(x)在点x1,x2处取得极值,且|x1
6);函数f(x)在点x1,x2处取得极值,且|x1 x2|=4.
x2|=4.
(1)求f(x)表达式;
(2)求函数f(x)在点P(3, 6)处切线方程.
6)处切线方程.
20.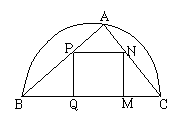 (满分14分)如图,某园林单位准备绿化一块直径为BC的半圆形空间,△ABC外的地方种草,△ABC的内接正方形MNPQ为水池,其余地方种花。若BC=a,∠ABC=
(满分14分)如图,某园林单位准备绿化一块直径为BC的半圆形空间,△ABC外的地方种草,△ABC的内接正方形MNPQ为水池,其余地方种花。若BC=a,∠ABC= ,设△ABC面积为S1,正方形MNPQ的面积为S2.
,设△ABC面积为S1,正方形MNPQ的面积为S2.
(1)用a,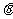 表示S1,S2;
表示S1,S2;
(2)当a固定,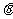 变化时,求
变化时,求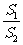 最小值及此时
最小值及此时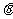 值.http://www.
值.http://www.
19.(满分14分)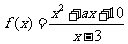 ,且x=1是f(x)的一个极值点.
,且x=1是f(x)的一个极值点.
(1)求a的值及f(x)单调区间;
(2))设g(x)=x3-3x-m2+4m,A={y | y=g(x),x∈[0,2]},B={y |y=f(x),x∈[0,2]}.若A∩B=B,求实数m的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com