
3.GoTo语句的认识及其他语句的进一步熟悉
[课堂互动]
问题:用区间二分法写出方程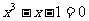 在区间[1,1.5]内的一个近似解(误差不超过0.001)的一个算法。
在区间[1,1.5]内的一个近似解(误差不超过0.001)的一个算法。
[算法设计思想]
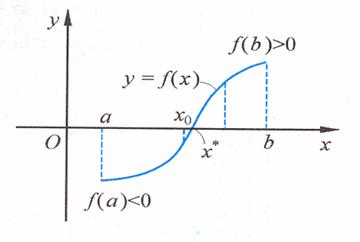
令函数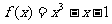 .如图,如果估计出方程
.如图,如果估计出方程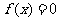 在某区间
在某区间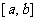 内有一个根
内有一个根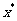 ,就能用二分法搜索求得符合误差限制
,就能用二分法搜索求得符合误差限制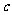 的近似解.
的近似解.
取[a,b]的中点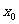 ,如果f(
,如果f(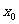 )=0,那么
)=0,那么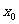 就是方程的根;否则判断根
就是方程的根;否则判断根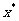 在
在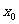 的左侧还是右侧,如果在左侧,就用[a,
的左侧还是右侧,如果在左侧,就用[a,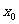 ]代替区间 [a,b]。如果在右侧,就用[
]代替区间 [a,b]。如果在右侧,就用[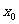 ,b]代替区间[a,b],如此循环下去,直到|a-b|<c(c是约定的误差范围,本例中为0.001)时终止,此时
,b]代替区间[a,b],如此循环下去,直到|a-b|<c(c是约定的误差范围,本例中为0.001)时终止,此时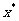 ≈
≈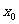 。
。
算法如下:
S1 取[a,b]的中点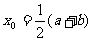 ,将区间一分为二;
,将区间一分为二;
S2 若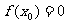 ,则
,则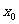 就是方程的根;否则判断根
就是方程的根;否则判断根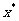 在
在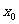 的左侧还是右侧:
的左侧还是右侧:
若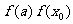 >0,则
>0,则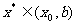 ,以
,以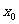 代替a;
代替a;
若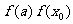 <0,则
<0,则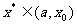 ,以
,以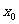 代替b;
代替b;
S3 若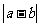 <c,计算终止,此时
<c,计算终止,此时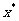 ≈
≈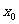 ,否则转S1。
,否则转S1。
[流程图]
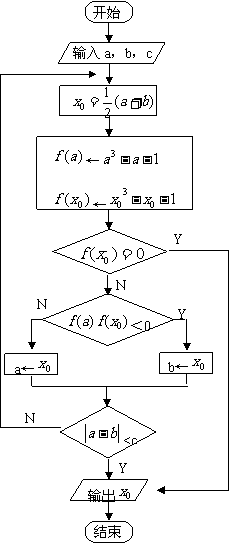
代码1:
Read a,b,c
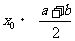
While 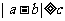 And
And 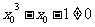
If 
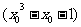 <0
<0
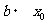
Else 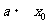
End If
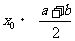
End While
Print 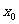
代码2:
10
Read 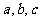
20 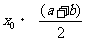
30 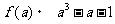
40 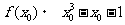
50 If 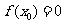 Then GoTo 120
Then GoTo 120
60 If 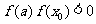 Then
Then
70
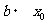
80 Else
90
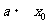
100 End If
110 If 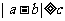 Then GoTo 20
Then GoTo 20
120 Print 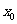
[追踪训练]
2.能由流程图分析出期所含有的结构并用为代码表示出相应的算法.
1.理解区间二分法的意义,二分法主要是采用了循环结构处理问题要会分析类似的问题;
4. 现有长度为360cm和780cm两种规格的钢筋若干.要焊接一批正方形模型.问怎样才能保证正方体体积最大且不浪费?
思路点拨: 正方体的所有棱长都相等,故必须将钢筋剪裁成长度相等的钢筋条;又必须不浪费,这就说明必须剪后无剩余.于是为了保证正方体的体积最大,故剪的钢筋的最大长度为360cm和780cm的最大公约数,可用更相减损术求最大公约数.
[解]
3.用更相减损法求下列各组数的最大公约数。
(31)72;168 (2)153;119
2.用辗转相除法求下列各组数的最大公约数。
(1)225;135 (2)98;196
1.分析下面一段代码的目的:
Read m,n
While m/n≠Int(m/n)
c←m- Int(m/n)×n
m←n
n←c
End While
Print n
(Int(x)表示不超过x的最大整数)
[解] 。
2. 更相减损法
我国早期也有解决求最大公约数问题的算法,就是更相减损术.
更相减损术求最大公约数的步骤如下:可半者半之,不可半者,副置分母之数,以少减多,更相减损,求其等也,以等数约之.
翻译出来为:
第一步:任意给出两个正数;判断它们是否都是偶数.若是,用2约简;若不是,执行第二步.
第二步:以较大的数减去较小的数,接着把较小的数与所得的差比较,并以大数减小数.继续这个操作,直到所得的数相等为止,则这个数(等数)就是所求的最大公约数.
再从这个角度看一下“求a=204,b=85的最大公约数”的问题,S1步可以等价为等式: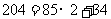 。S2步可以等价为等式:
。S2步可以等价为等式: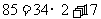 。这两步从减法的角度可以理解为:204-85,所得的差与减式中的较小数比较,再用大的数减小的数,循环执行以上步骤,直到结果为0。此时减数就是a和b的最大公约数。这一算法根据它的特点,也可以用循环语句完成。
。这两步从减法的角度可以理解为:204-85,所得的差与减式中的较小数比较,再用大的数减小的数,循环执行以上步骤,直到结果为0。此时减数就是a和b的最大公约数。这一算法根据它的特点,也可以用循环语句完成。
参考代码:
/a放较大的数,b放较小的数
If a < b Then
m ← a
a ← b
b ← m /交换a,b中的数
End If /确保a是a,b中较大的数
r ← a – b /两数相减
While r ≠ 0
If b > r Then
a ← b
b ← r
Else
a ← r
End If
r ← a – b
/确保相减后仍用较大的数减去较小的数
End While
Print b
用“更相减损法”求多于两个数的最大公约数就可以显示出其优越性
[小结]比较辗转相除法与更相减损术的区别
(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显.
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到.
[追踪训练]
1.辗转相除法
公元前3世纪,欧几里得介绍了求两个正整数a,b(a>b)的最大公约数的方法,求出一列数: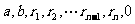 ,这列数从第三项开始,每一项都是前两项相除所得的余数(即
,这列数从第三项开始,每一项都是前两项相除所得的余数(即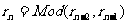 ),余数等于0的前一项
),余数等于0的前一项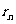 ,即是a和b的最大公约数,这种方法称为“欧几里得辗转相除法”。
,即是a和b的最大公约数,这种方法称为“欧几里得辗转相除法”。
例1 求两个正数8251和6105的最大公约数.
(分析:8251与6105两数都比较大,而且没有明显的公约数,如能把它们都变小一点,根据已有的知识即可求出最大公约数)
[解]8251=6105×1+2146
显然8251和2146的最大公约数也必是2146的约数,同样6105与2146的公约数也必是8251的约数,所以8251与6105的最大公约数也是6105与2146的最大公约数.
6105=2146×2+1813
2146=1813×1+333
1813=333×5+148
333=148×2+37
148=37×4+0
则37为8251与6105的最大公约数.
[小结]以上我们求最大公约数的方法就是欧几里得辗转相除法.其求最大公约数的步骤如下:
第一步:用较大的数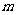 除以较小的数
除以较小的数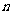 得到一个商
得到一个商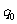 和一个余数
和一个余数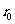 ;
;
第二步:若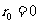 ,则
,则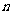 为
为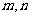 的最大公约数;若
的最大公约数;若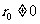 ,则用除数
,则用除数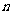 除以余数
除以余数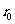 得到一个商
得到一个商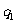 和一个余数
和一个余数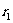 ;
;
第三步:若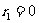 ,则
,则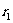 为
为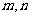 的最大公约数;若
的最大公约数;若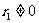 ,则用除数
,则用除数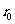 除以余数
除以余数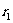 得到一个商
得到一个商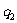 和一个余数
和一个余数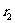 ;
;
……
依次计算直至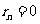 ,此时所得到的
,此时所得到的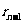 即为所求的最大公约数.
即为所求的最大公约数.
[练习]求a=204,b=85的最大公约数,步骤为:
S1
S2
S3
所以它们的最大公约数为 。
算法描述:计算出a÷b的余数r,若r=0,则b为a,b的最大公约数;若r≠0,则把前面的除数b作为新的被除数,把余数r作为新的除数(a,b要重新赋值,a←b,b←r),继续进行上述运算,直到余数为0(用While循环语句,循环的执行条件是r≠0,当r=0时,循环终止),此时的除数即为所求的最大公约数。
算法如下:
S1 输入两个正整数a,b(a>b);
S2 若Mod(a,b)=0,则转S3;否则,r←Mod(a,b), a←b,b←r,转S2。
S3 输出最大公约数b;
[流程图]
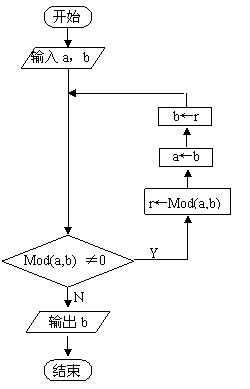
[伪代码]

2.基本能根据算法语句与程序框图的知识设计完整的程序框图并写出算法程序.
[课堂互动]
问题:
写出求两个正整数a,b(a>b)的最大公约数的一个算法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com