
2.用辗转相除法求85和51的最大公约数时,需要做除法的次数为___3_______.
1. 下面是一个算法的伪代码.如果输入的x的值是20,则输出的y的值是( D )
A.100 B.50
C.25 D.150
|
4.用秦九韶算法计算多项式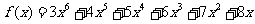 在
在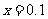 时的值时,需要做乘法和加法的次数分别是 ( D )
时的值时,需要做乘法和加法的次数分别是 ( D )
A. 6 , 6 B. 5 , 6
C. 5 , 5 D. 6 , 5
[经典范例]
例1 把求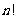 的程序补充完整.(提示:n!=1×2×…×n)
的程序补充完整.(提示:n!=1×2×…×n)
|
[解]分别填入 Read,While,End While.
例2 用秦九韶算法求多项式
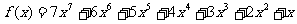 在
在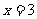 时的值.
时的值.
[解]
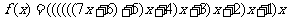

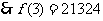
例3 用二分法求方程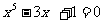 在
在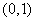 上的近似解,精确到
上的近似解,精确到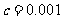 ,写出算法
,写出算法 画出流程图.
画出流程图.
[解]算法如下:
S1
取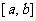 中点
中点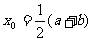 ,将区间一分为二
,将区间一分为二
S2
若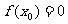 ,则
,则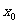 就是方程的根;否则所求根
就是方程的根;否则所求根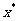 在
在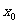 的左侧或右侧
的左侧或右侧
若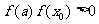 ,则
,则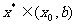 ,以
,以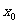 代替
代替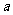 ;
;
若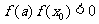 ,则
,则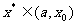 ,以
,以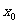 代替
代替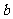 ;
;
S3 若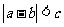 ,计算终止,此时
,计算终止,此时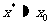 ,否则转到第1步
,否则转到第1步
流程图:(注:将程序框图中所有“:=”换成“←”)
[追踪训练]
3.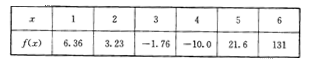 已知
已知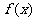 的图象是连续不断的,
的图象是连续不断的,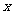 与
与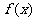 的对应值如下表所示:
的对应值如下表所示:
则函数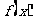 一定存在根的区间有 ( C )
一定存在根的区间有 ( C )
A.[1,2]和[2,3] B.[2,3]和[3,4]
C.[2,3]和[4,5] D.[3,4]和[4,5]
2.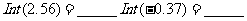
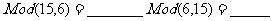 答案: 2,-1,3,6
答案: 2,-1,3,6
1. 我国古代数学发展一直处于世界领先水平,特别是宋、元时期的“算法”,其中可以同欧几里德辗转相除法相媲美的是( B )
A.割圆术 B.更相减损术
C.秦九韶算法 D.孙子剩余定理
2.能运用基本算法语言表示顺序、选择、循环这三种基本结构;能进行初步的综合应用.
[自学评价]
1. 进一步巩固基本算法语句:赋值语句、输入输出语句、条件语句、循环语句的概念,并掌握其结构.
1.在直角坐标系中作出函数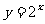 和
和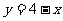 的图象,根据图象判断方程
的图象,根据图象判断方程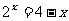 的解的范围,再用二分法求这个方程的近似解(误差不超过0.001),并写出这个算法的伪代码,画出流程图。
的解的范围,再用二分法求这个方程的近似解(误差不超过0.001),并写出这个算法的伪代码,画出流程图。
[解]由图像可知方程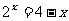 有一个根在[1,2]内。
有一个根在[1,2]内。
a←1
b←2
c←0.001
While 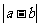 ≥c
≥c
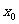 ←(a+b)/2
←(a+b)/2
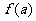 ←
←
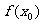 ←
←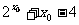
If 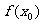 =0 Then Exit While
=0 Then Exit While
If 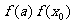 <0
Then
<0
Then
b←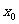
Else
a←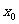
End If
End While
Print 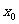
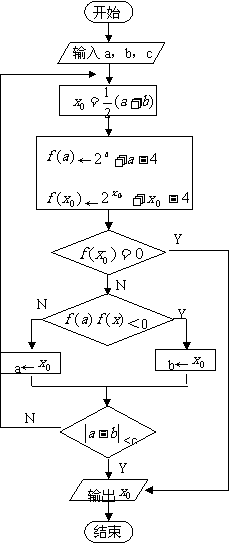 流程图如下:
流程图如下:
3.GoTo语句的认识及其他语句的进一步熟悉。
[课堂互动]
问题:用区间二分法写出方程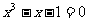 在区间[1,1.5]内的一个近似解(误差不超过0.001)的一个算法。
在区间[1,1.5]内的一个近似解(误差不超过0.001)的一个算法。
算法设计思想:
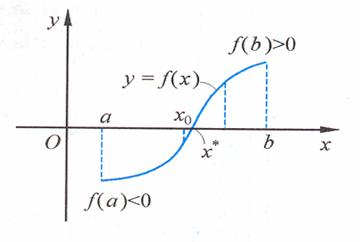
令函数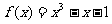 .如图,如果估计出方程
.如图,如果估计出方程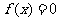 在某区间
在某区间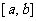 内有一个根
内有一个根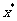 ,就能用二分法搜索求得符合误差限制
,就能用二分法搜索求得符合误差限制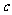 的近似解.
的近似解.
取[a,b]的中点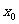 ,如果f(
,如果f(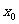 )=0,则
)=0,则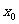 就是方程的根;否则判断根
就是方程的根;否则判断根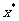 在
在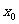 的左侧还是右侧,如果在左侧,就用[a,
的左侧还是右侧,如果在左侧,就用[a,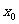 ]代替区间 [a,b]。如果在右侧,就用[
]代替区间 [a,b]。如果在右侧,就用[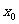 ,b]代替区间[a,b],如此循环下去,直到|a-b|<(c是约定的误差范围,本例中为0.001)时终止,此时
,b]代替区间[a,b],如此循环下去,直到|a-b|<(c是约定的误差范围,本例中为0.001)时终止,此时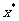 ≈
≈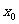 。
。
算法步骤:
S1 取[a,b]的中点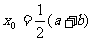 ,将区间一分为二;
,将区间一分为二;
S2 若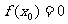 ,则
,则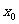 就是方程的根;否则判断根
就是方程的根;否则判断根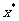 在
在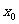 的左侧还是右侧:
的左侧还是右侧:
若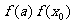 >0,则
>0,则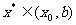 ,以
,以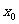 代替a;
代替a;
若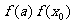 <0,则
<0,则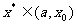 ,以
,以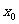 代替b;
代替b;
S3 若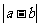 <c,计算终止,此时
<c,计算终止,此时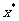 ≈
≈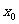 ,否则转S1。
,否则转S1。
[流程图]
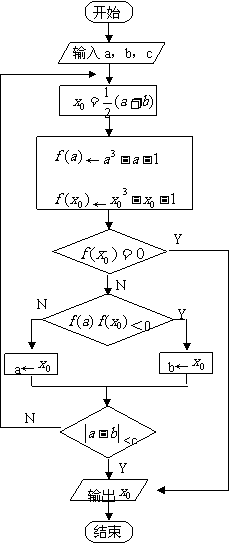
[伪代码]代码1:
Read a,b,c
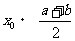
While 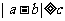 And
And 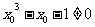
If 
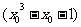 <0
<0
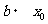
Else 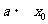
End If
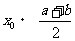
End While
Print 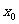
代码2:
10
Read 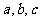
20 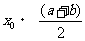
30 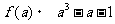
40 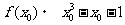
50 If 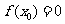 Then GoTo 120
Then GoTo 120
60 If 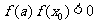 Then
Then
70
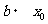
80 Else
90
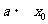
100 End If
110 If 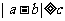 Then GoTo 20
Then GoTo 20
120 Print 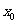
[追踪训练]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com