1、　 《练习册》 P 21、22

4、　　 体会二次函数是某些实际问题的数学模型

教学重点和难点

重点：理解a与c的图象的影及响图象的开口方向、对称轴和顶点坐标

难点：理解a与c的图象的影及响图象的开口方向、对称轴和顶点坐标

教学过程设计

一、　　　　 从学生原有的认知结构提出问题

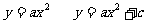在上一节课，我们研究了最简单的二次函数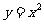和的图象。这节课，我们将接着讨论形如　　　 和　　　　　 的图象的作法和性质，以及a与c的图象的影响。

二、　　　　 师生共同研究形成概念

1、 刹车距离与二次函数

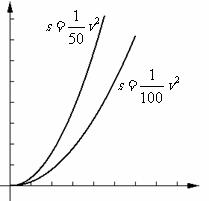刹车距离是二次函数关系的应用之一，本节借助晴天和雨天刹车距离的不同，引出二次函数的系数对图象的影响。

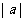越大，开口越小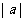；越小，开口越大

两个图象的相同之处：

两者都位于s轴的右侧；

函数值都随v值的增大而增大；

2、 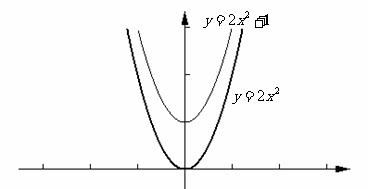a与c的取值对图象的影响

☆　 做一做　 书本P 44　 做一做

此图象可由学生自己完成。鼓励学生用自己的语言

进行描述。二次函数的图象是抛物线；二次函数的

图象形状相同，但顶点坐标不同；把二次函数的

图象向上、向下、向左、向右平移后，就可以

得到不同的二次函数的图象。

当时，抛物线的开口向上；

当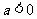时，抛物线的开口向下。

当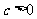时，抛物线与y轴的交点在原点的上方；

当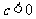时，抛物线与y轴的交点在原点的下方。

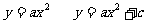
3、 　　　　和　　　　　 的图象的开口方向、对称轴和顶点坐标

☆　 议一议　　 书本P 45　 议一议

1)　　 形状、开口方向、对称轴都相同，但顶点坐标不同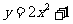，的图象的顶点坐标是(0 ，1)，实际上，只要将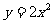的图象向上平移1个单位，就可以得到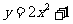的图象；

2)　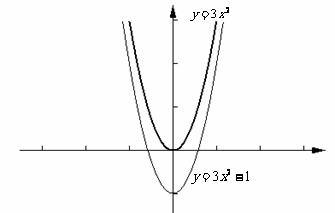　 两二次函数的形状、开口方向、对称轴都相同，但顶点坐标不同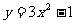，的图象的顶点坐标是(0 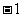，)，实际上，只要将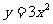的图象向上平移1个单位，就可以得到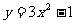的图象。

4、 讲解例题

例1　　　 《练习册》 P 21　 7。

三、　　　　 随堂练习

3、　　 能说出　　　 和　　　　　 的图象的开口方向、对称轴和顶点坐标

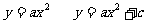
2、　　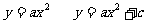　 能作出　　　 和　　　　　 的图象，并能够比较它们与　　　 的异同，理解a与c的图象的影响

1、　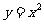　　 经历探索二次函数　　　 和　　　　　 的图象的作法和性质的过程，进一步获得将表格、表达式、图象三者联系起来的经验