
3.设计算法流程图,输出200以内除以3余1的正整数。
解:流程图如下:(将“=”换成“←”)
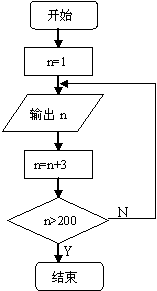
2.请观察给出的流程图(如下图),这是一个求和算法的流程图,请运行几步看一看,指出该循环结构的循环体、循环变量和循环的终止条件。
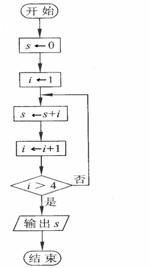
[解]s,i为循环变量;终止条件为i>4
1.下图给出的是计算
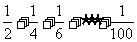 的值的一个程序框图,其中判断框内应填入的条件是( B )
的值的一个程序框图,其中判断框内应填入的条件是( B )
A. i>100 B. i≤100
C. i>50 D. i≤50
1.进一步理解循环结构的执行过程,并能进行简单的综合应用.
[课堂互动]
自学评价
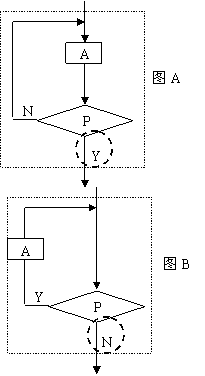
我们学习的循环结构分两种基本类型: 直到型循环和当型循环.
图A中,循环体一直执行,直到条件成立时退出循环,这种循环称为直到型循环。
图B中,当条件成立时循环体才执行,这种循环称为当型循环。
[经典范例]
例1设计算法,输出1 000以内能被3和5整除的所有正整数,画出算法流程图。
[解] (点拨:凡是能被3和5整除的正整数都是15的倍数,由于1 000=15×66+10,因此1 000以内一共有66个这样的正整数。)
流程图如下:
例2 斐波拉契数列表示的是这样的一列数:0,1,1,2,3,5,…,后一项等于前两项的和。设计一个算法流程图,输出这个数列的前50项。
[解]
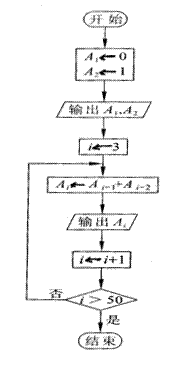
例3 先分步写出计算2+4+6+…+100的一个算法,再画出流程图(使用循环结构)。
[解]算法如下:
S1 S←0
S2 I←2
S3 S←S+I
S4 I←I+2
S5 I是否大于100,如果是,转S6;否则转S3
S6 输出S。
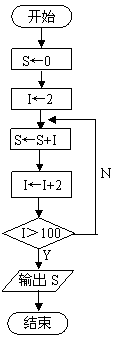
[追踪训练]
3. 用
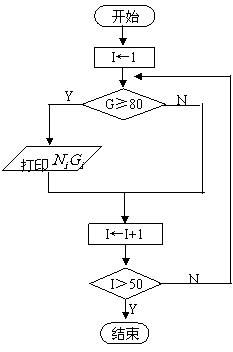
用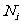 代表第i个学生的学号,
代表第i个学生的学号,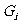 代表第i个学生的成绩(i=1,2,…,50),下图表示了一个什么样的算法?
代表第i个学生的成绩(i=1,2,…,50),下图表示了一个什么样的算法?
[解]输出学号在1到50号之间成绩大于等于80的学生的学号和成绩。
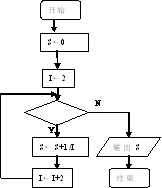
2.有如下程序框图(如下图所示),
则该程序框图表示的算法的功能是
(将“=”换成“←”)
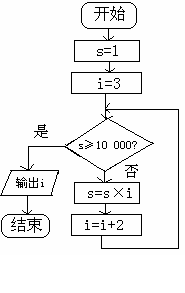
解:求使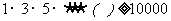 成立的最小正整数n的值加2。
成立的最小正整数n的值加2。
1. 算法的三种基本结构是 ( A )
A . 顺序结构、选择结构、循环结构
B. 顺序结构、流程结构、循环结构
C. 顺序结构、分支结构、流程结构
D. 流程结构、循环结构、分支结构
2.
写出求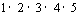 值的一个算法。
值的一个算法。
算法一:
S1 先求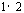 ,得到
,得到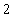 ;
;
S2 将S1得到的结果再乘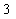 ,得到
,得到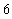 ;
;
S3 将S2得到的结果再乘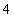 ,得到
,得到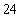 ;
;
S4 将S3得到的结果再乘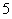 ,得到最后的结果
,得到最后的结果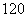 。;
。;
[思考]如果一直乘到100,上述算法有何弊端,有通用性吗?
算法二:
S1 设一个变量T←1;
S2 设另一个变量为i←2;
S3 T←T×i { 将T×i的结果仍放在变量T中 };
S4 i←i+1 {i的值增加1};
S5 如果i不大于5,转S3,否则输出T,算法结束。
[比较] 算法二与算法一相比有何优越性?
这个方法可以在条件限制中加入任意的值来,比如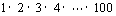 也可以用同样的程序来执行,只要修改一下限制条件即可。
也可以用同样的程序来执行,只要修改一下限制条件即可。
流程图:
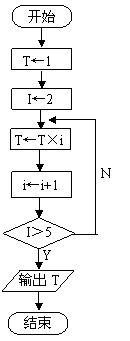
[思考]将算法二作如下修改,注意与算法二的区别。
算法三:
S1 设一个变量T=1
S2 设另一个变量为i=2
S3 如果i不大于5,T←T×i ,执行S4,否则转到S5
S4 i←i+1,重复S3
S5 输出T
分析:在算法三中,执行S3、S4是有条件的,当i小于等于5时才可以。
流程图:
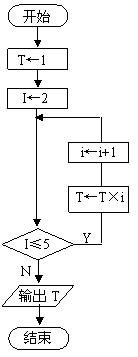
上述循环结构用示意图表示为:
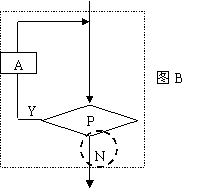
[总结]图A中,循环体一直执行,直到条件成立时退出循环,这种循环称为直到型循环。图B中,当条件成立时循环体才执行,这种循环称为当型循环。
[经典范例]
例1 设计一个计算10个数的平均数的算法。
[分析]我们用一个循环依次输入10个数,再用一个变量存放数的累加和,在求出10个数的总和后,除以10,就得到这10个数的平均数。
[解]算法如下:
S1 S←0
S2 I←1
S3 输入G {输入一个数}
S4 S←S+G {求S+G,其和仍放在S中}
S5 I←I+1
S6 如果I不大于10,转S3 {如果I>10不成立,开始循环}
S7 A←S/10 {将平均数S/10存放到A中}
S8 输出A
流程图:
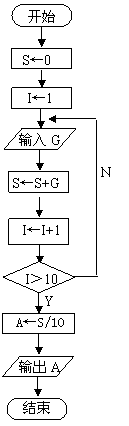
[追踪训练]
1.问题 北京获得了2008年的奥运会的主办权,你知道在申办奥运会的最后阶段时,国际奥委会是如何通过投票来决定主办权归属的吗?
对五个申报的城市进行表决的程序是:首先进行的第一轮投票,如果有哪一个城市得票超过半数,那么该城市将获得举办权,表决结束;如果所有的申报城市的票数都没有半数,则将得票最少的城市淘汰,然后重复上述过程,直到选出一个申办城市为止。
你能用一个算法来表达上述过程吗?
算法:
S1:投票
S2:统计票数,如果有一个城市的票数超过半数,那么该城市当选,获得主办权,转S3;否则,淘汰得票数最少的城市,转S1;
S3:宣布主办城市。
上述算法用流程图如下所示:
[小结] 在该算法中,在主办城市没有出来之前,“投票并淘汰得票最少的城市”这一操作将会重复执行,直到有一个城市获半数以上的票。像这种需要重复执行同一操作的结构称为循环结构(cycle structure)。
[注意] 粗体字部分是循环结束的条件,即直到该条件成立(或为“真”)时循环才结束。
用流程图可表示为(注意圆卷部分是循环结束的条件)。
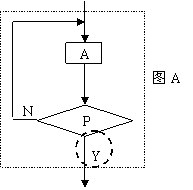
3.理解当型循环与直到型循环在流程图上的区别,通过分析理解两种循环方式在执行过程上的区别。
[课堂互动]
自学评价
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com