
4. 若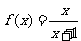 ,则f (1)+f (2)+…+f (2002)+f
(2003)+f (1)+f (
,则f (1)+f (2)+…+f (2002)+f
(2003)+f (1)+f (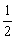 )+…+f (
)+…+f (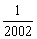 )+f (
)+f (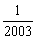 )=_______.
)=_______.
解析:∵f(x)+f(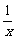 )=
)=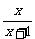 +
+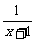 =1, ∴原式=2003×1=2003. 答案:2003
=1, ∴原式=2003×1=2003. 答案:2003
3. 设函数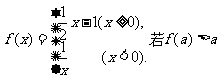 ,则实数a的取值范围是 ____ .
,则实数a的取值范围是 ____ .

2. 设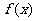 是R上的任意函数,则下列叙述正确的是( D )
是R上的任意函数,则下列叙述正确的是( D )
A.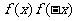 是奇函数 B.
是奇函数 B.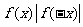 是奇函数
是奇函数
C.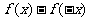 是偶函数
D.
是偶函数
D. 是偶函数
是偶函数
1. 下列函数中在 上单调递减的是( A )
上单调递减的是( A )
(A)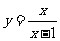 (B)
(B)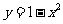 (C)
(C)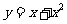 (D)
(D)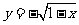
13.
解:解:∵f(x)是偶函数,且x>0,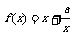 ,
,
∴x<0时,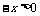 ,
,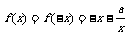
∵f(x)在 单调递减,在
单调递减,在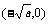 单调递增
单调递增
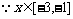 ,
,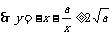 ,当且仅当
,当且仅当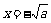 时取等号.
时取等号.
而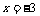 时,
时,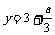 ;
;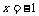 时,
时,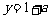
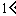 若
若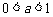 ,
,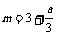 ,
,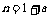 ,
,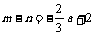
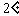 若
若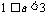 ,∴f(x)在
,∴f(x)在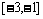 上最大值为
上最大值为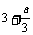 ,最小值为
,最小值为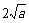
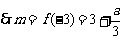 ,
,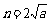 ,
,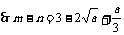
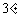 若
若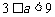 ,
,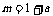 ,
,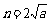 ,则
,则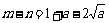
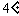 若
若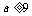 ,
,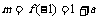 ,
,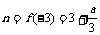 ,
,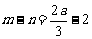

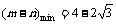 (当a=3时取最小值)
(当a=3时取最小值)
13. 已知y=f(x)是偶函数,当x>0时,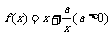 ,且当
,且当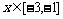 时,
时,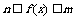 恒成立,
用含有
恒成立,
用含有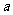 的式子表示
的式子表示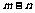 .
.
12. 已知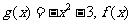 为二次函数,且
为二次函数,且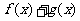 为奇函数,当
为奇函数,当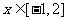 时,
时,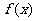 的
的
最小值为1,求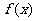 的解析式 .
的解析式 .
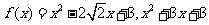
11. 已知函数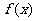 满足,对任意的
满足,对任意的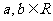 都有
都有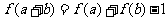 ,且当
,且当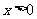 时,有
时,有
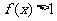 .(1)求证:
.(1)求证: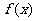 是
是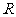 上的增函数;(2)若
上的增函数;(2)若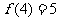 ,解不等式
,解不等式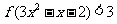 .
.
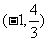
10. 讨论函数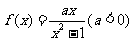 的单调性 .
的单调性 .
设-1<x1<x2<1,则f(x2)-f(x1)=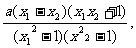
∴ 当a<0时,f(x)在(-1,1),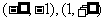 上为增函数,
上为增函数,
9. 已知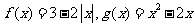 ,构造函数
,构造函数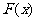 ,定义如下:当
,定义如下:当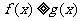 时,
时,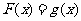 ,当
,当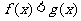 时,
时, 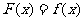 .那么
.那么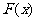 ( A )
( A )
A.有最大值7-2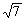 , 无最小值
B. 有最大值3, 最小值
, 无最小值
B. 有最大值3, 最小值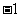
C.有最大值3, 无最小值 D.无最大值, 也无最小值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com