
6.已知一元二次方程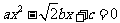 的两个根满足
的两个根满足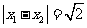 ,且a,b,c分别是
,且a,b,c分别是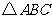 的∠A,∠B,∠C的对边.若
的∠A,∠B,∠C的对边.若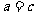 ,求∠B的度数.小敏解得此题的正确答案“
,求∠B的度数.小敏解得此题的正确答案“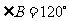 ”后,思考以下问题,请你帮助解答.
”后,思考以下问题,请你帮助解答.
(1)若在原题中,将方程改为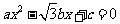 ,要得到
,要得到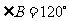 ,而条件“
,而条件“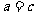 ”不变,那么对应条件中的
”不变,那么对应条件中的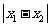 的值作怎样的改变?并说明理由.
的值作怎样的改变?并说明理由.
(2)若在原题中,将方程改为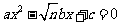 (n为正整数,
(n为正整数,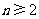 ),要得到
),要得到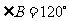 ,而条件“
,而条件“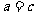 ”不变,那么条件中的
”不变,那么条件中的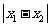 的值应改为多少(不必说明理由)?
的值应改为多少(不必说明理由)?
5.青青商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件恰好用去2 700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润(利润=售价-进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案;
(3)在“五·一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
|
打折前一次性购物总金额 |
优惠措施 |
|
不超过300元 |
不优惠 |
|
超过300元且不超过400元 |
售价打九折 |
|
超过400元 |
售价打八折 |
按上述优惠条件,若小王第一天只购买甲种商品一次性付款200元,第二天只购买乙种商品打折后一次性付款324元,那么这两天他在该商场购买甲、乙两种商品一共多少件?(通过计算求出所有符合要求的结果)
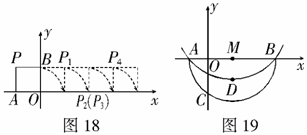
4.如图19,设抛物线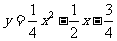 交x轴于
交x轴于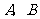 两点,顶点为
两点,顶点为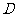 .以
.以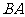 为直径作半圆,圆心为
为直径作半圆,圆心为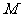 ,半圆交y轴负半轴于
,半圆交y轴负半轴于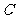 .
.
(1)求抛物线的对称轴;
(2)将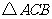 绕圆心
绕圆心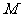 顺时针旋转
顺时针旋转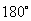 ,得到
,得到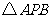 ,如图20.求点
,如图20.求点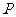 的坐标;
的坐标;
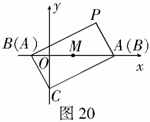
(3)有一动点 在线段
在线段 上运动,
上运动,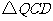 的周长在不断变化时是否存在最小值?若存在,求点
的周长在不断变化时是否存在最小值?若存在,求点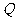 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
3.如图18,将边长为1的正方形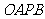 沿x轴正方向连续翻转2 008次,点
沿x轴正方向连续翻转2 008次,点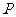 依次落在点
依次落在点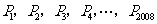 的位置,则
的位置,则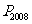 的横坐标
的横坐标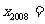 ________.
________.
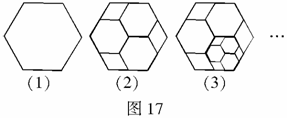
2.将图17(1)所示的正六边形进行分割得到图17(2),再将图17(2)中最小的某一个正六边形按同样的方式进行分割得到图17(3),再将图17(3)中最小的某一个正六边形按同样的方式进行分割…,则第n个图形中,共有________个正六边形.
1.观察算式:
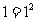 ;
;
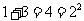 ;
;
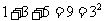 ;
;
 ;
;
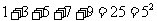 ;……
;……
用代数式表示这个规律(n为正整数):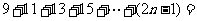 ________.
________.
21.解:(1)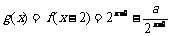 …………
…………
(2)设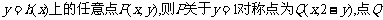
在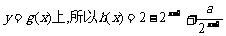 ………………………
………………………
(3)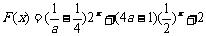 ………………………
………………………
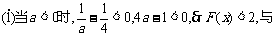 题设矛盾
题设矛盾
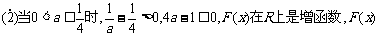 无最小值:
无最小值:
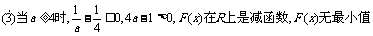
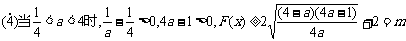
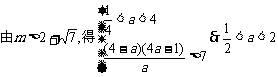 ……………………
……………………
20.解:(1)∵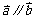 ,∴
,∴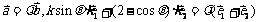 ,
,
∴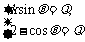 ∴
∴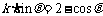 ,
,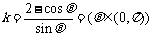 .
.
(2)
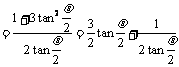 .
.
又∵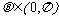 ,∴
,∴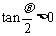 .
.
∴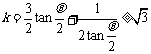 (当且仅当
(当且仅当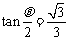 ,即
,即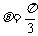 时取等号)
时取等号)
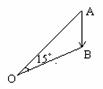
19.解:如图:设科比能截住球,科比启动点为A,O为传球点, B为接球点,
从传球到接着球的时间为t,球速为v,则∠AOB=15°,OB=vt,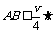 。
。
在△AOB中,由正弦定理,得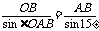 ,
,
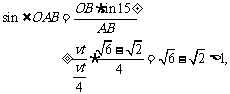
故不能截住球.
18.解:(1)∵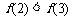 ,∴
,∴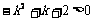 ,即
,即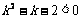 ,
,
∵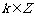 ,∴
,∴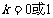
(2)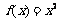 ,
, 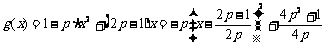
当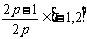 ,即
,即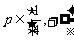 时,
时,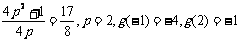
当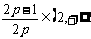 时,∵
时,∵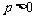 ,∴这样的
,∴这样的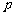 不存在。
不存在。
当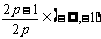 ,即
,即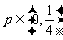 时,
时,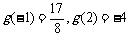 ,这样的
,这样的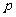 不存在。
不存在。
综上得,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com