2．探究：在坐标系中a、b角构造a+b角

1．探究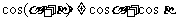

反例：

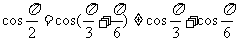
问题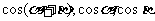：的关系？

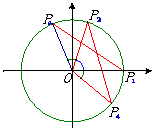解决思路：探讨三角函数问题的最基本的工具是直角坐标系中的单位圆及单位圆中的三角函数线

3．培养探索和创新的能力和意识.

[自学评价]

2、应用公式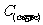，求三角函数值.

1、理解向量法推导两角和与差的余弦公式，并能初步运用解决具体问题；

3.1两角和与差的三角函数

第1课时

[学习导航]

学习要求

3. 运用上述公式进行简单的恒等变换，推导半角公式，积化和差、和差化积公式作为基本训练，进一步提高运用转化的观点去处理问题的自觉性，体会一般与特殊的思想，换元的思想，方程的思想等数学思想在三角恒等变换中的应用。

2. 理解以两角差的余弦公式导出两角和与差的正弦、余弦、正切公式，二倍角的正弦、余弦、正切公式，了解它们的内在联系；

1. 了解用向量的数量积推导出两角差的余弦公式的过程，进一步体会向量方法的作用；

3、三角恒等变换具有几何和物理的应用背景。以向量为桥梁将三角恒等变换的算式与直观的几何图形相互沟通和转化，有助于学习和应用三角恒等变换，还能提高学习数学的兴趣，体会数学是一个有机联系的整体，而不是各不相关的内容的堆积。

知识结构　

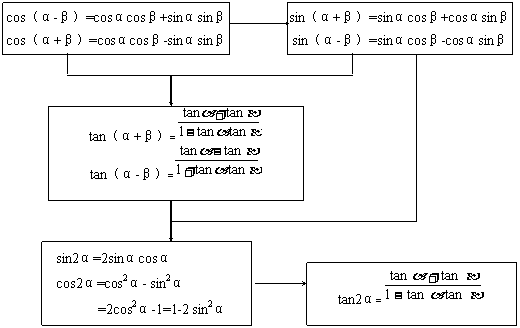
学习要求