
7.已知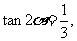 求
求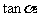 的值.
的值.
[师生互动]
|
学生质疑 |
|
|
教师释疑 |
|
6.已知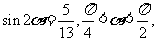 求
求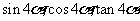 的值.
的值.
5.已知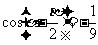 ,
,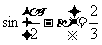 ,
,
且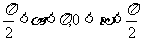 ,求
,求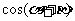 的值。
的值。
4. 已知
已知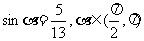 ,求sin2a,cos2a,tan2a的值.
,求sin2a,cos2a,tan2a的值.
3.求值
(1)sin10°sin30°sin50°sin70°
(2) cos200cos400cos600cos800
2.求值:
(1)sin22°30’cos22°30’=
(2)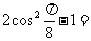
(3)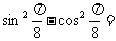
(4)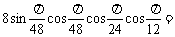
例6求证:
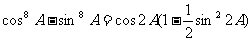
[解]
例7求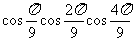 的值。
的值。
[解]
进一步探讨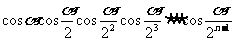 的值。
的值。
思维点拔:
要理解并掌握二倍角公式以及推导,能正确运用二倍角的正弦、余弦、正切公式进行简单三角函数式的化简、求值与恒等式证明.
二倍角公式是由和角公式由一般化归为特殊而来的,要注重这种基本数学思想方法,学会怎样去发现数学规律.
[追踪训练]:
1.若270°<α<360°,则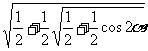 等于 ( )
等于 ( )
A.sin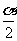 B.cos
B.cos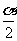
C.-sin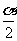 D.-cos
D.-cos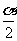
之间的关系
例5已知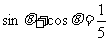 ,
,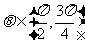 ,求
,求 ,
,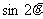 ,
,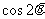 ,
,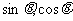 的值。
的值。
[解]
2、进一步体会“化归思想”(三倍角化归为两角和与二倍角)。
例4已知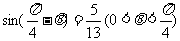 ,求
,求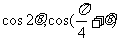 的值。
的值。
[解]
点评:进一步体会角的变换的妙处。
例1不查表.求下列各式的值
(1)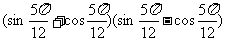 (2)
(2)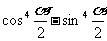
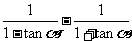
(3)
(4)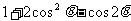
[解]
例2若tan q = 3,求sin2q - cos2q 的值
[解]
例3用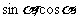 表示
表示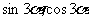
[解]
点评:
1、加深对“二倍角”的理解,即角的变换;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com