
8、如图是由几个小立方块所搭几何体的俯视图 ,小正方形中的数字表示在该位置的小立方块的个数,这个几何体的主视图是 ( )
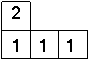
 A.
A.
 B.
B.
 C.
C.
 D.
D.

7、下列四个几何体中,主视图、左视图与俯视图是全等图形的几何体是( )
A、球 B、圆柱 C、三棱柱 D、圆锥
6、如图所示的正四棱锥的俯视图是( )

5、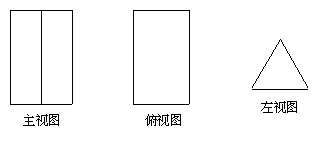 如果某物体的三视图是如图所示的三个图形,
如果某物体的三视图是如图所示的三个图形,
那么该物体的形状是 ( )A、正方体 B、长方体 C、三棱柱 D、圆锥
4、一空间几何体的三视图如图所示,则这个几何体是( )
A、圆柱 B、圆锥 C、球 D、长方体
3、 我们从不同的方向观察同一物体时,可以看到不同的平面图形,如图,从图的左面看这个几何体的左视图是( )
我们从不同的方向观察同一物体时,可以看到不同的平面图形,如图,从图的左面看这个几何体的左视图是( )





A B C D
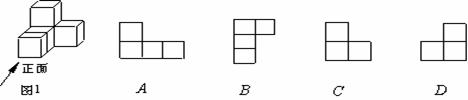
2、图1中几何体的主视图是( )
1.下列空间图形中是圆柱的为( )
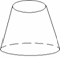
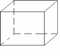


(A) (B) (C) (D)
21.解:(1)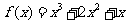 ,则
,则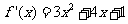 . ..............1分
. ..............1分
令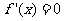 解得:
解得: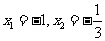 ,
..............2分
,
..............2分
|
x |
(-¥, -1) |
-1 |
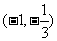 |
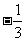 |
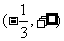 |
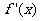 |
+ |
0 |
- |
0 |
+ |
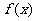 |
↗ |
极大值0 |
↘ |
极小值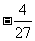 |
↗ |
∴ f(x)的极大值为f(-1)=0, 极小值为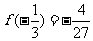 .
..........4分
.
..........4分
(2)若最大值b与最小值a均在端点处取得,则有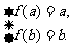 或
或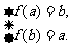 ...5分
...5分
① 当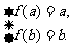 时,则a, b即为方程f(x)
= x的解,解得x1 = 0, x2 = -2.
时,则a, b即为方程f(x)
= x的解,解得x1 = 0, x2 = -2.
当-2≤x≤0时,-2≤f(x)≤0,检验知符合题意. ...........6分
② 当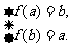 时,则有
时,则有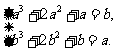
相减得: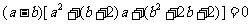 .
.
又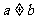 ,而方程
,而方程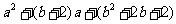 = 0中
= 0中
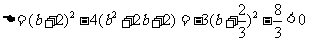 ,方程无解,故此时a,b不存在.
,方程无解,故此时a,b不存在.
............8分
若最大值b在区间(a,b)内取得,则b必为f(x)的极大值0,但b=0时f(b)=b,矛盾.
若最小值a在区间(a,b)内取得,则a必为f(x)的极小值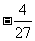 ,但f(x)在区间
,但f(x)在区间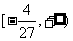 上单调递增,必有f(a)=a,矛盾.
上单调递增,必有f(a)=a,矛盾.
综上得:a = -2, b = 0. .............10分
(3)易知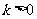 ,
,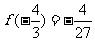 .
.
若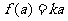 ,则
,则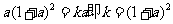 ,而此时
,而此时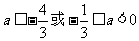 .
.
当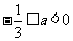 时,
时,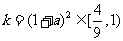 ,此时k有最小值为
,此时k有最小值为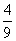 .
.
当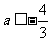 时,
时,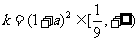 ,此时k有最小值
,此时k有最小值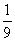 . ........12分
. ........12分
若最小值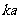 在区间
在区间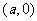 内取得,则
内取得,则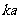 必为f(x)的极小值,即
必为f(x)的极小值,即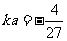 ,而此时
,而此时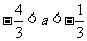 ,∴
,∴ 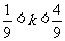 .
.
综上得:k的最小值为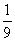 ,此时
,此时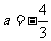 .
..............14分
.
..............14分
20.解:(1)由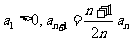 知,
知,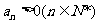 ,故
,故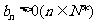 .
.
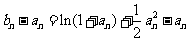 ,
..................2分
,
..................2分
设函数 ,则当x>0时,
,则当x>0时,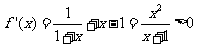 ,
,
∴ f(x)在[0, +¥)上是增函数,
∴ 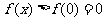 ,即
,即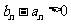 ,∴
,∴ 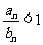 . ................4分
. ................4分
∵ 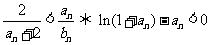 .
.
设函数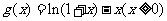 ,则当x>0时,
,则当x>0时,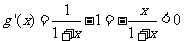 ,
,
∴ g(x)在[0,+¥)上是减函数,故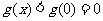 ,
,
∴ 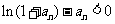 .
.......................6分
.
.......................6分
综上得: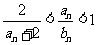 .
.................7分
.
.................7分
(2)由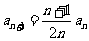 得:
得: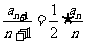 ,
,
∴ 数列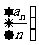 是以1为首项,以 为公比的等比数列,
是以1为首项,以 为公比的等比数列,
∴ 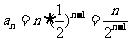 ,
...............9分
,
...............9分
∵ 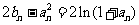 ,由(1)的结论有
,由(1)的结论有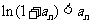 ,
,
∴ 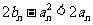 ,
...............11分
,
...............11分
∴ 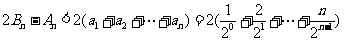 .
.
令Sn = 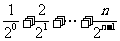 ,则
,则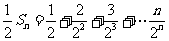 ,相减得:
,相减得:
 ,
,
∴ 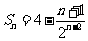 ,
................13分
,
................13分
∴ 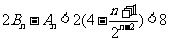 .
.................14分
.
.................14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com