
4.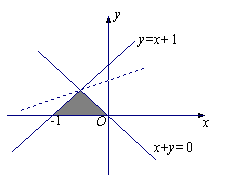 B.解析:假设有一组数值
B.解析:假设有一组数值 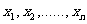 (皆为实数),其平均值为:
(皆为实数),其平均值为: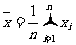 ,此组数值的标准差为:
,此组数值的标准差为: 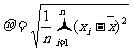 .
.
3.D.解析:根据向量的和、差的意义.
2.B.解析:集合A={0, 1},集合B={x | 0<x<2},故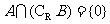 .
.
1.A.解析: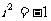 ,
,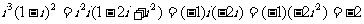 .
.
21.(本小题满分14分)已知函数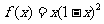 .
.
(1)求函数f(x)的极值;
(2)求实数a, b的值,使在区间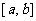 上的值域也为
上的值域也为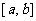 ;.
;.
(3)是否存在区间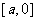 ,使f(x)在区间
,使f(x)在区间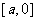 上的值域为
上的值域为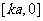 ,且使k的值最小?若存在,求出k的最小值及此时a的值;若不存在,请说明理由.
,且使k的值最小?若存在,求出k的最小值及此时a的值;若不存在,请说明理由.
[答案及详细解析]
20.(本小题满分14分)设数列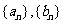 满足
满足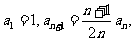 且
且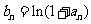
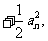
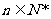 .
.
(1)证明: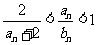 ;
;
(2)记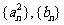 的前n项和分别为An, Bn,证明:2Bn
- An < 8.
的前n项和分别为An, Bn,证明:2Bn
- An < 8.
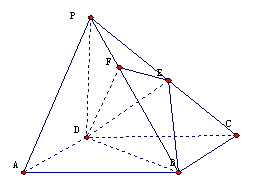
19.(本小题满分14分)如图,在四棱锥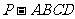 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱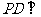 底面ABCD,
底面ABCD,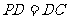 ,E是PC的中点,作
,E是PC的中点,作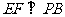 交PB于点F.
交PB于点F.
(I) 证明: PA∥平面EDB;
(II) 证明:PB⊥平面EFD;
(III) 求二面角B-DE-F的余弦值.
18.(本小题满分14分)已知动圆与直线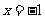 相切,且过定点F(1, 0),动圆圆心为M.
相切,且过定点F(1, 0),动圆圆心为M.
(1)求点M的轨迹C的方程;
(2)若直线l与曲线C交于A、B两点,且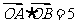 (O为坐标原点),求证:直线l过一定点.
(O为坐标原点),求证:直线l过一定点.
17.(本小题满分12分)甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为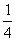 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为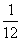 ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为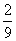 .
.
(Ⅰ)分别求甲、乙、丙三台机床各自加工零件是一等品的概率;
(Ⅱ)甲、乙、丙各加工一个零件,求一等品零件数x 的数学期望.
16.(本小题满分12分)已知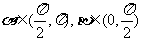 ,且
,且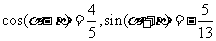 ,求
,求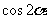 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com