
1. 两角和的正弦公式的推导
sin(a+b)=cos[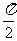 -(a+b)]
-(a+b)]
=cos[(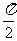 -a)-b]
-a)-b]
=cos(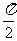 -a)cosb+sin(
-a)cosb+sin(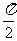 -a)sinb
-a)sinb
=sinacosb+cosasinb
即: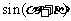

以-b代b得:
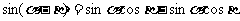
2 公式的分析,结构解剖:正余余正符号同。
公式的分析,结构解剖:正余余正符号同。
[精典范例]
 例1求值
例1求值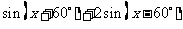
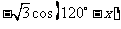
[解]
例2 :已知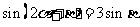 ,
,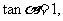 求
求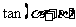 的值.
的值.
例3已知sin(a+b)=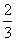 ,sin(a-b)=
,sin(a-b)=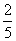 求
求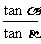 的值.
的值.
[解]
例4(1)已知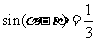 ,
,
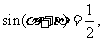 求tanα: tanβ的值.
求tanα: tanβ的值.
[解]
思维点拔:
由两角和的余弦公式推导出两角和的正弦公式,并进而推得两角和的正弦公式,并运用进行简单的三角函数式的化简、求值和恒等变形。
[追踪训练一]:
3. 掌握诱导公式
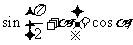
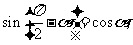
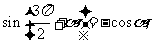
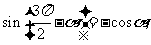
重点难点
重点:由两角和的余弦公式推导出两角和的正弦公式
难点:进行简单的三角函数式的化简、求值和恒等变形
[自学评价]
2. 通过公式的推导,了解它们的内在联系,培养逻辑推理能力。
并运用进行简单的三角函数式的化简、求值和恒等变形。
1. 掌握两角和与差的正弦公式及其推导方法。
5.利用两角和与差的余弦公式证明下列诱导公式:
(1)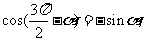
(2)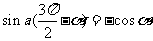
(3)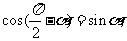
(4)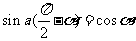
[师生互动]
4.化简: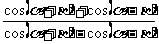
= 。
3.已知cosα= ,α∈(,2π),则cos(α-)= 。
2. 若
若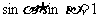 ,则
,则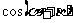 的值为 ( )
的值为 ( )
A. 0 B. 1 C.  D. -1
D. -1
1.满足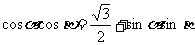 的一组
的一组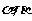 的值是 ( )
的值是 ( )
A. 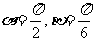 B.
B. 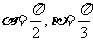
C. 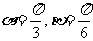 D.
D. 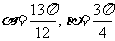
6.已知cos(a-b)=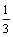 ,求(sina+sinb)2+(cosa+cosb)2的值.
,求(sina+sinb)2+(cosa+cosb)2的值.
[选修延伸]
例5已知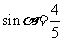 ,
,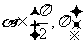
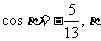 是第三象限角,求
是第三象限角,求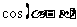 的值.
的值.
例6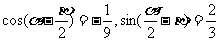 ,
,
且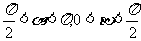 ,
,
求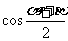 的值.
的值.
[追踪训练]:
|
学生质疑 |
|
|
教师释疑 |
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com