
1.设集合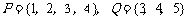 ,全集
,全集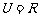 ,则集合
,则集合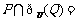 ( )
( )
A.{1,2} B.{3,4}
C.{1} D.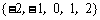
2、 《练习册》 P 59
四、 小结
圆与圆的位置关系;圆心距与两圆半径和两圆的关系。
五、 作业
书本 P 130 习题3.9 1
六、 教学后记
1、 书本 P 128 随堂练习
21. 解:(1)由于点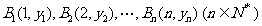 在直线
在直线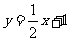 上,
上,
则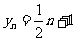 ,
……1分
,
……1分
因此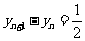 ,所以数列
,所以数列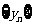 是等差数列.
……2分
是等差数列.
……2分
(2)由已知有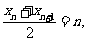 ,那么
,那么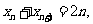 ……3分
……3分
同理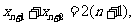
以上两式相减,得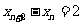 ,
……4分
,
……4分
∴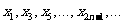 成等差数列;
成等差数列;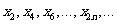 也成等差数列,
也成等差数列,
∴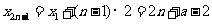 ,
……5分
,
……5分
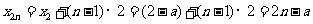 ,
……6分
,
……6分
点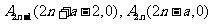 ,则
,则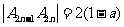 ,
,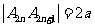 ,
,
而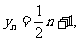 ∴
∴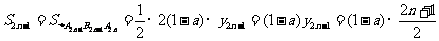 . ……8分
. ……8分
(3)由(1)得: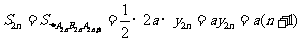 ,
……9分
,
……9分
则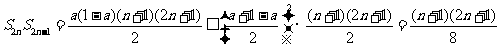 ,
,
而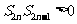 ,则
,则 ,
……11分
,
……11分
即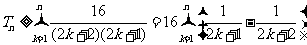 ,
,
∴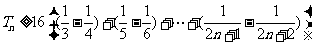 ,
,
∴ ,
,
∴ ,
……12分
,
……12分
由于 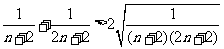 ,
,
而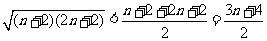 ,
,
则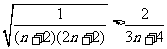 , 从而
, 从而 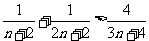 ,
……13分
,
……13分
同理: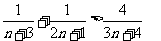 ,
,
……
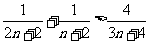 ,
,
以上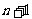 个不等式相加得:
个不等式相加得: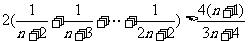 ,
,
即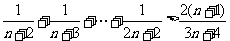 ,
,
从而 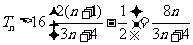 .
……14分
.
……14分
说明:(1)也可由数学归纳法证明 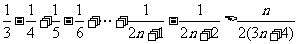 ;
;
(2)本题也可以求出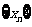 的通项公式,由
的通项公式,由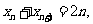 两边同时除以
两边同时除以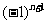 ,
,
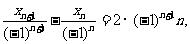
令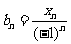 ,则
,则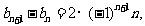
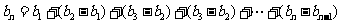
 ,
,
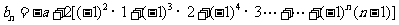
 ,
,
利用错位相减法可求出:
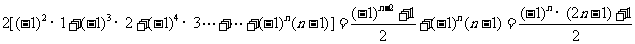 ,
,
则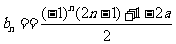 ,
,
则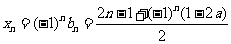 ,
,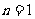 时,也符合上式,
时,也符合上式,
则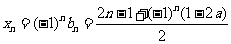 对任意正整数
对任意正整数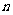 都成立.
都成立.
下同上述解法.
20.解:依题意,曲线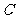 为抛物线,且点
为抛物线,且点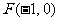 为抛物线的焦点,
为抛物线的焦点,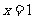 为其准线, ……2分
为其准线, ……2分
则抛物线形式为 ,由
,由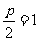 ,得
,得 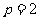 ,
……4分
,
……4分
则曲线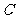 的方程为
的方程为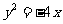 .
……6分
.
……6分
(2)设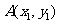 ,
,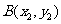 ,假设存在点
,假设存在点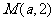 满足条件,则
满足条件,则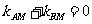 ……8分
……8分
即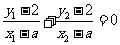 ,即
,即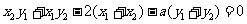 ,
① ……9分
,
① ……9分
而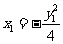 ,
,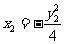 ,
②
,
②
整理得 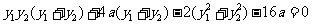 ,
,
即为: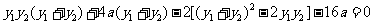 ,
③ ……11分
,
③ ……11分
由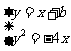 得:
得: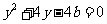 ,
,
则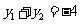 ,
,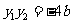 , ④
……12分
, ④
……12分
将④代入③得: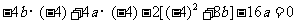 ,即
,即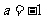 . ……13分
. ……13分
因此,存在点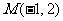 满足题意. ……14分
满足题意. ……14分
19. 解:(1)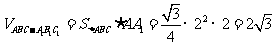 ,
……3分
,
……3分
(2)建立如图空间坐标系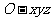 ,设
,设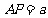 ,
……4分
,
……4分
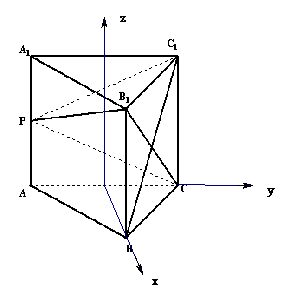 则
则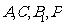 的坐标分别为
的坐标分别为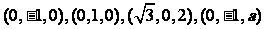 ; ……6分
; ……6分
∴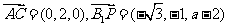
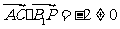 ,
,
∴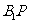 不垂直
不垂直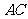 ;
;
∴直线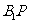 不可能与平面
不可能与平面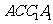 垂直;
……8分
垂直;
……8分
(3)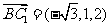 ,由
,由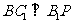 ,得
,得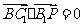 ,
,
即
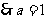 ;
;
又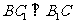
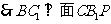 ;
;
∴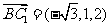 是面
是面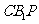 的法向量;
……10分
的法向量;
……10分
设面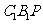 的法向量为
的法向量为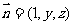 ,
,
由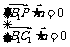 得
得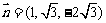 ,
……12分
,
……12分
设二面角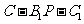 的大小为
的大小为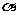 ,则
,则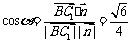 ,
,
∴二面角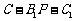 的余弦值大小为
的余弦值大小为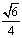 .
……14分
.
……14分
说明:有些结果由于法向量的方向问题,出现余弦值为负值者扣1分.
18. 解:(1)当a = -1时,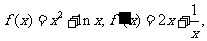 ……1分
……1分
∴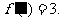
函数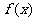 在点x
= 1处的切线方程为y-1= 3(x-1),即y =3x -2
……3分
在点x
= 1处的切线方程为y-1= 3(x-1),即y =3x -2
……3分
当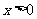 时,
时,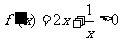 ,∴函数
,∴函数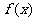 在(0,+∞)上是增函数,
在(0,+∞)上是增函数,
而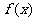 的定义域为
的定义域为 ,则函数
,则函数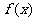 的单调增区间为
的单调增区间为 ,不存在递减区间. ……5分
,不存在递减区间. ……5分
(2)函数 的定义域为(0,+∞),
的定义域为(0,+∞),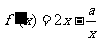 ,
……6分
,
……6分
①当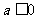 时,
时,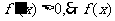 在(0,+∞)上是增函数;函数
在(0,+∞)上是增函数;函数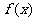 无极值
……8分
无极值
……8分
②当 时,由
时,由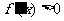 ,得
,得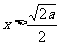 ,
……9分
,
……9分
由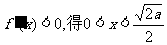 ,
……10分
,
……10分
∴当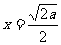 时,
时,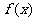 有极小值
有极小值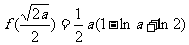 ……11分
……11分
综上,当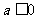 时,
时,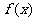 无极值;当
无极值;当 时,
时,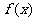 有极小值
有极小值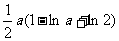 ,无极大值……12分
,无极大值……12分
17. 解:(1)周销售量为2吨,3吨和4吨的频率分别为0.2,0.5和0.3. ……3分
(2)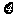 的可能值为8,10,12,14,16,
……4分
的可能值为8,10,12,14,16,
……4分
P(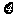 =8)=0.22=0.04, P(
=8)=0.22=0.04, P(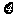 =10)=2×0.2×0.5=0.2, ……6分
=10)=2×0.2×0.5=0.2, ……6分
P(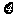 =12)=0.52+2×0.2×0.3=0.37, P(
=12)=0.52+2×0.2×0.3=0.37, P(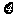 =14)=2×0.5×0.3=0.3,
=14)=2×0.5×0.3=0.3,
P(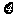 =16)=0.32=0.09.
……9分
=16)=0.32=0.09.
……9分
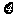 |
8 |
10 |
12 |
14 |
16 |
|
P |
0.04 |
0.2 |
0.37 |
0.3 |
0.09 |
则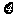 的分布列为
的分布列为
……11分 =8×0.04+10×0.2+12×0.37+14×0.3+16×0.09=12.4(千元).
……13分
=8×0.04+10×0.2+12×0.37+14×0.3+16×0.09=12.4(千元).
……13分
说明:第(1)问每个频率1分,第(2)问一种情况的概率1分,分布列正确2分,期望2分.
16. 解:(1)由于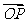
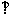
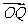 ,则
,则 ,
………………3分
,
………………3分
显然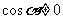 ,两边同时除以
,两边同时除以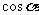 得,
得,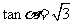 ;
………………6分
;
………………6分
(2)由于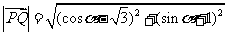 ,
………………8分
,
………………8分
即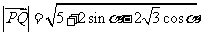 ,
,
∴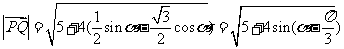 ………………10分
………………10分
由于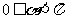 ,则
,则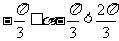 ,
………………11分
,
………………11分
则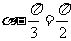 ,即
,即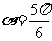 时,
时, 最大值为
最大值为 .
………………13分
.
………………13分
说明:本题第(1)问可以利用解析几何两直线垂直的条件求出,第(2)问可以结合平面几何知识得出.
(二)选做题(13-15题,考生只能从中选做两题)
13. 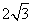 .解析:将其化为直角坐标方程为
.解析:将其化为直角坐标方程为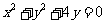 ,和
,和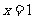 ,代入得:
,代入得: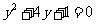 ,
,
则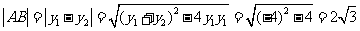 .
.
14. .解析:由题设
.解析:由题设 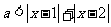 对任意实数
对任意实数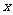 均成立,由于
均成立,由于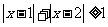 ,则
,则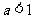 .
.
15.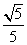 .解析:由射影定理得
.解析:由射影定理得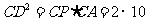 ,
,
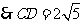 ,则cos∠ACB=sin∠A=
,则cos∠ACB=sin∠A=
sin∠D=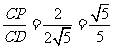 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com