
若题目中既限定了起始反应进行的方向,又要求确定某物质起始用量的范围,那么既要使用过程假设(即假设起始反应按指定方向进行),又要使用程度假设(即假设原平衡不发生移动,或假设各物质的起始量就是原平衡量)。
例4
在一定温度和压强下,把2体积N2和6体积H2通入一个体积可变的密闭容器中,发生反应N2(g)+3H2(g)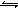 2NH3(g),达到平衡后测得混合气体为7体积。若规定起始时反应向逆反应方向进行,用a、b、c分别表示N2、H2、NH3的起始体积数,则c的取值范围是 。
2NH3(g),达到平衡后测得混合气体为7体积。若规定起始时反应向逆反应方向进行,用a、b、c分别表示N2、H2、NH3的起始体积数,则c的取值范围是 。
解析 通过计算知,平衡时N2、H2、NH3的体积数分别为1.5、4.5、1。若a=1.5、b=4.5、c=1,则起始时反应不向任何方向进行;若起始时反应从逆反应方向开始,则a=b=0,c=4。故1<c≤4。
练习
1.一定条件下,可逆反应X(g)+3Y(g) 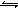 2Z(g),若X、Y、Z的起始浓度(mol/L)分别为c1、c2、c3(均不为零),当达到平衡时,X、Y、Z的浓度(mol/L)分别为0.1、0.3、0.08,则c1的取值范围是 。
2Z(g),若X、Y、Z的起始浓度(mol/L)分别为c1、c2、c3(均不为零),当达到平衡时,X、Y、Z的浓度(mol/L)分别为0.1、0.3、0.08,则c1的取值范围是 。
化学平衡研究的对象是可逆反应,可逆反应是不能向某方向进行到底的,但在确定反应向某方向进行所需某物质某种量的取值范围,或在确定混合体系某种量的总量或平均量时,可对反应进行的程度作出极端假设,这种假设称为程度假设。程度假设须是在限定了反应进行的方向时使用,其假设也有两种情况,一是假设反应不向任何方向进行或原平衡不再发生移动,即假设各物质的起始量就是原平衡量,二是假设反应向指定方向进行到底,即假设不足量的物质会耗尽,从而求得两个(或一个)极端值,但所得取值范围不可取“=”号。另外,题目中对反应进行方向的限定,有直接的和间接的(即隐含的),间接的限定可能是反应只向正(或逆)反应方向进行,也可能既可以向正反应方向进行,又可以向逆反应方向进行,解题时应仔细辨析。
例2
在一个容积不变的反应器中,要求通过调节体系的温度使反应A(g)+2B(g) 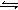 2C(g)达到平衡时,保持容器中气体的总物质的量为12 mol。现向反应器中加入6.5 mol A、x mol B、2.0mol C,欲使起始反应维持向逆反应方向进行,则x的取值范围是 。
2C(g)达到平衡时,保持容器中气体的总物质的量为12 mol。现向反应器中加入6.5 mol A、x mol B、2.0mol C,欲使起始反应维持向逆反应方向进行,则x的取值范围是 。
解析 若起始时反应不向任何方向进行,则6.5+x+2.0=12。x=3.5;若反应向逆反应方向进行到底,2.0 mol C可生成1.0 mol A和2.0 mol B,则(6.5+1.0)+(x+2.0)=12,x=2.5。故2.5<x<3.5。
 A(g)+B(g)
A(g)+B(g)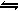 2C(g)
D(g)+2E(g)
2C(g)
D(g)+2E(g)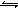 2F(g)
2F(g)
例3 在一个容积固定的反应器中,有一可左右滑动的密封隔板,两侧分别进行如图所示的可逆反应。各物质的起始加入量是:A、B、C均为4.0mol,D为6.5 mol,F为2.0mol。设E为x mol,当x在一定范围内变化时,可以通过调节反应器的温度,使两侧反应都达到平衡,并且隔板恰好处于反应器的正中间位置,则x的取值范围是 。
解析 该题乍看好象跟上例相同,因为左侧为等气体物质的量反应,总物质的量也为12mol,右侧反应的特点及起始用量也相同。但是,本题并未限定右侧反应起始进行的方向,由于x为不确定的数,这其实就隐含着起始反应可能向正反应方向进行,也可能向逆反应方向进行。若反应向正反应方向进行到底,由于6.5 mol D完全转化可生成13mol F,已超过12mol,应使x mol E完全转化,可消耗x/2 mol D生成x mol F,则(6.5-x/2)+(2.0+x)=12,x=7.0;若反应向逆反应方向进行到底,由上例知x=2.5。故2.5<x<7.0。
在一定条件下,化学平衡的建立,可以从正反应方向开始,也可以从逆反应方向开始,只要起始投料相当,都可以达到相同的平衡状态。即化学平衡的建立与反应条件有关,与反应发生的途径无关。若不限定反应的起始方向,在确定某物质起始用量的范围时,可对反应发生的过程或平衡建立的途径作出假设,这种假设称为过程假设或途径假设。使用时可作出两种情况的假设,一是假设反应从正反应方向开始,二是假设反应从逆反应方向开始,从而分别求得这两种情况下的极端值。若物质的起始用量可以为零,则所确定的取值范围可以取“=”号,否则不可取“=”号。
例1
一定条件下,可逆反应A(g)+B(g)  2C(g)达到平衡后,测得c(A)=0.5mol/L,c(B)=0.1mol/L,c(C)=1.6mol/L。若A、B、C的起始浓度(mol/L)分别以a、b、c表示,则a的取值范围是 。
2C(g)达到平衡后,测得c(A)=0.5mol/L,c(B)=0.1mol/L,c(C)=1.6mol/L。若A、B、C的起始浓度(mol/L)分别以a、b、c表示,则a的取值范围是 。
解析 若反应从正反应方向开始,把1.6molC换算得A为0.8mol,则A的起始浓度最大可为0.5+0.8=1.3 mol/L;若反应从逆反应方向开始,由于A相对于B过量,使0.1mol的B完全反应需A为0.1mol,剩余A的浓度最小为0.5-0.1=0.4 mol/L,故0.4≤a≤1.3。同理,0≤b≤0.9,0≤c≤1.8。
22. 设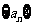 是等差数列,从
是等差数列,从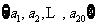 中任取3个不同的数,使这3个数仍成等差数列,则这样不同的等差数列最多有(C)
中任取3个不同的数,使这3个数仍成等差数列,则这样不同的等差数列最多有(C)
A.90 B.120 C.180 D.200
21. 用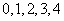 排成数字可重复的五位数, 其中中间三位数字各不相同, 但首末两位数字相同的五位数共有(B)
排成数字可重复的五位数, 其中中间三位数字各不相同, 但首末两位数字相同的五位数共有(B)
A. 480个 B. 240个 C. 96个 D. 48个
20. 某天的课程表要求上午排四节课, 下午排两节课, 其中语文、数学各排两节, 英语、生物各排一节, 且数学、语文必须连排(即数学与数学相邻, 语文与语文相邻, 上午第四节与下午第一节视为不相邻), 并且语文和数学不能相邻, 则不同的安排方法有(B)
A. 24种 B. 12种 C. 4种 D. 48种
19. 用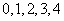 这五个数字组成无重复数字的五位数, 其中恰有一个偶数夹在两个奇数之间的五位数共有 个. 28
这五个数字组成无重复数字的五位数, 其中恰有一个偶数夹在两个奇数之间的五位数共有 个. 28
18. 设直线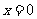 和
和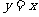 将圆
将圆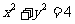 分成4部分, 用5种不同的颜色给四部分涂色, 要求每部分涂一种且相邻部分不能为同种颜色, 则不同的涂色方案有(C)
分成4部分, 用5种不同的颜色给四部分涂色, 要求每部分涂一种且相邻部分不能为同种颜色, 则不同的涂色方案有(C)
A. 120种 B. 240种 C. 260种 D. 280种
17.在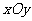 平面上,顶点坐标
平面上,顶点坐标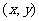 满足
满足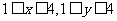 ,且
,且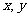 是整数的三角形有(
是整数的三角形有( )
)
 .
.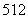 个
个
 .
.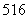 个
个
 .
.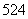 个
个
 .
.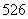 个
个
16.三个人踢毽,互相传递,每人每次只能踢一下,由甲开始踢,经过 次传递后,毽又被踢回给甲,则不同的传递方式共有(
次传递后,毽又被踢回给甲,则不同的传递方式共有( )
)
 .6种
.6种
 .
. 种
种
 .
.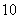 种
种
 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com