
3.已知关于x的方程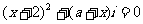 有实根b,且
有实根b,且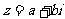 ,则
,则 = ( )
= ( )
A.2+2i B.-2+2i C.2-2i D.-2-2i


 1.函数y=x-3和y=log3x的定义域分别是P、Q,则 ( )
1.函数y=x-3和y=log3x的定义域分别是P、Q,则 ( )
A. B.
B. ; C.
; C. RQ=P D.
RQ=P D. RP=
RP=
2.已知不等式|8x+9|<7和不等式ax2+bx>2的解集相同,则实数a、b的值分别为 ( )
A.-8、-10 B.-4、-9 C.-1、9 D.-1、2
作业:《教学与测试》第31课 练习题
2.设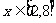 ,函数
,函数 的最大值是1,最小值是
的最大值是1,最小值是
 ,求
,求 的值。
的值。
解: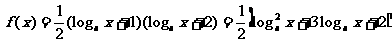

由题设,∵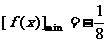 这时
这时 
又∵ ∴
∴
∵ 是关于
是关于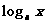 的二次函数,
的二次函数,
∴函数最大值或最小值必在 时取得
时取得
若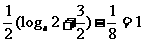 则
则
∵取得最小值时  这时
这时 舍去
舍去
若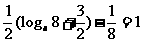 则
则 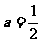 此时取得最小值时
此时取得最小值时
 符合题意
符合题意
∴ 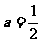
1.若 ,求
,求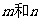 的关系。
的关系。
解:原式可以化为 
当 且
且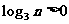 时,即
时,即
∵底数 ∴
∴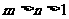
当 且
且 时,即
时,即
∵底数 ∴
∴
当 且
且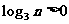 时,
时, 
综上所述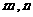 的关系为
的关系为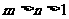 或
或 或
或
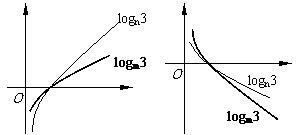
 实际上三种情况可用图形表示:
实际上三种情况可用图形表示:
题目:比较下列两个对数的大小
1.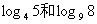 2.
2.
( )
(
)
( )
)
5.已知:矩形ABCD所在平面为α,点P∈α,但P  BC.作PQ⊥平面α,问:点P在什么位置时,∠QCB分别是(1)直角,(2)锐角,(3)钝角,并加以证明.
BC.作PQ⊥平面α,问:点P在什么位置时,∠QCB分别是(1)直角,(2)锐角,(3)钝角,并加以证明.
(提示:利用cosθ1·cosθ2=cosθ公式)
3.将正方形ABCD沿对角线BD折起来,使A点在平面BCD的射影O恰好在BD上,又CD的中点为E,求证:AE⊥CD.
(提示:对于平面BCD来说,AO是垂线,OE是斜线AE在平面上的射影)

AB=13,AC=15,A1B=5,A1C=9.试比较∠BAC与∠BA1C的大小.(提示:用余弦定理可得∠BAC=∠BA1C)
2.已知:在△ABC中,∠BAC=90°,PC⊥△ABC所在平面,D为AB上一点,PA,PD,PB与平面ABC分别成60°,45°,30°的角,求证:D是AB的中点.
1.已知:正方形ABCD的边长为10,O为正方形中心,PO⊥平

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com