
6.(Ⅰ)f(α)f(β)=-4. (Ⅱ)设α<x1<x2<β, 则f(x1)-f(x2)= {(x1-x2)[a(x1+x2)-4x1x2+4]}/[(x12+1)(x22+1)]. ∵ α、β为方程2x2-ax-2=0的二根,
∴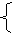 |
α+β=(1/2)a, |
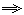 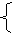 |
a=2(α+β), |
|
αβ=-1 |
1=-αβ. |
∴ a(x1+x2)-4x1x2+4=2[(α+β)(x1+x2)-2x1x2-2αβ]=2[(x1-α)(β-x2)+(x2-α)(β-x1)]>0, ∴ f(x1)<f(x2), 即函数f(x)在[α,β]上递增.
10.假设存在等腰直角△ABC,则|AC|=|BC|,AC⊥BC.不妨设A、B分居于y轴的左、右两侧(在同侧是不可能的).设CA的斜率为k,则k>0,CB的斜率为-(1/k).CA的方程为y=kx+1,代入椭圆方程并整理得(a2k2+1)x2+2a2kx=0,∴ x=0或x=-(2a2k)/(a2k2+1),∴ |CA|=(2a2k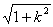 )/(a2k2+1).以-(1/k)代k,得?|CB|=(2a2
)/(a2k2+1).以-(1/k)代k,得?|CB|=(2a2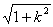 )/(a2+k2).由|CA|=|CB|,得(k-1)[k2-(a2-1)k+1]=0(?).方程(?)至少有解k=1.故等腰直角△ABC总存在,个数等于方程(?)的正数解的个数.当1<a≤
)/(a2+k2).由|CA|=|CB|,得(k-1)[k2-(a2-1)k+1]=0(?).方程(?)至少有解k=1.故等腰直角△ABC总存在,个数等于方程(?)的正数解的个数.当1<a≤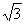 ,(?)仅有一个解(或称三个相同的解);当a>
,(?)仅有一个解(或称三个相同的解);当a>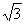 ,(*)有三个不同的解, ∴符合题设的△ABC一定存在,最多有3个.
?§?5 怎样答高考综合题
1.(i)若按原来投资环境,由p=-(1/160)(x-40)2+10知,当x=40时,p大=10,即10年的总利润的最大值为100万元.
(ii)若对该产品开发,前5年可用于对该产品的投资只有30万元,而函数p=-(1/160)(x-40)2+10在(0,30]上递增.∴ 当x=30时,p大=(75/8),前5年的总和的最大利润为(375/8)万元.
设后5年,x万元用于本地销售投资,60-x万元用于异地销售投资,则总利润为W=[10-(1/160)(x-40)2]×5+(-(159/160)x2+(119/2)x)×5=5[900-(x-30)2],
∴ 当x=30时,W大=4500,
即十年的总利润的最大值为(375/8)+4500.
显然(375/8)+4500>100,故该产品具有极大的开发价值.
,(*)有三个不同的解, ∴符合题设的△ABC一定存在,最多有3个.
?§?5 怎样答高考综合题
1.(i)若按原来投资环境,由p=-(1/160)(x-40)2+10知,当x=40时,p大=10,即10年的总利润的最大值为100万元.
(ii)若对该产品开发,前5年可用于对该产品的投资只有30万元,而函数p=-(1/160)(x-40)2+10在(0,30]上递增.∴ 当x=30时,p大=(75/8),前5年的总和的最大利润为(375/8)万元.
设后5年,x万元用于本地销售投资,60-x万元用于异地销售投资,则总利润为W=[10-(1/160)(x-40)2]×5+(-(159/160)x2+(119/2)x)×5=5[900-(x-30)2],
∴ 当x=30时,W大=4500,
即十年的总利润的最大值为(375/8)+4500.
显然(375/8)+4500>100,故该产品具有极大的开发价值.
2.(1)由题意得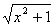 ≤1+ax,原不等式等价于 ≤1+ax,原不等式等价于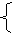 |
x≥0, |
|
(a2-1)x+2a≥0. |
当0<a<1时,解集为{x|0≤x?≤(2a)/(1-a2)};当a>1时,不等式解集为{x|x≥0}.?
(2)设x1,x2∈[0,+∞),且x1<x2.
f(x1)-f(x2)=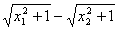 -a(x1-x2)
=(x1-x2)([(x1+x2)/
-a(x1-x2)
=(x1-x2)([(x1+x2)/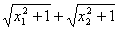 ]-a)
∵ (x1-x2)<(x1+x2)/
]-a)
∵ (x1-x2)<(x1+x2)/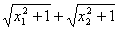 <1,
(1)当a≥1时,f(x1)-f(x2)>0,即f(x1)>f(x2),
故当a≥1时,函数f(x)在区间[0,+∞)上是单调递减函数.
(2)当0<a<1时,函数f(x)在区间[0,+∞)上不是单调函数.
综上,当且仅当a≥1时,函数f(x)在区间[0,+∞)上是单调函数.
3.设M=sin220°+cos250°+sin20°cos50°,
N=cos220°+sin250°+cos20°sin50°,
则 M+N=2+sin70°, ①
M-N=-cos40°+cos100°-sin30°
=-2sin70°sin30°-sin30°
=-sin70°-(1/2). ②
由①+②,得2M=(3/2).故M=(3/4).
4.(1)根据平移规律,得
C1:y-s=(x-t)3-(x-t).
(2)在曲线C上任取B1(x1,y1),设B2(x2,y2)是关于A的对称点,则(x1+x2/2)=(t/2),(y1+y2)/2=(s/2),所以x1=t-x2,y1=s-y2,代入C的方程,得s-y2=(t-x2)3-(t-x2),即y2-s=(x2-t)3-(x2-t),可知B2(x2,y2)在曲线C1上,同理C1上的点关于点A的对称点在曲线C上.因此,曲线C与C1关于点A对称.
5.(1)x1=(a/2),y1=(b/2).
(2)xn=a/(n+1),yn=(b/n+1).
(3)由Zn=xn·yn+1=a/(n+1)·b/(n+2)=(1/(n+1)-1/(n+2))ab,
<1,
(1)当a≥1时,f(x1)-f(x2)>0,即f(x1)>f(x2),
故当a≥1时,函数f(x)在区间[0,+∞)上是单调递减函数.
(2)当0<a<1时,函数f(x)在区间[0,+∞)上不是单调函数.
综上,当且仅当a≥1时,函数f(x)在区间[0,+∞)上是单调函数.
3.设M=sin220°+cos250°+sin20°cos50°,
N=cos220°+sin250°+cos20°sin50°,
则 M+N=2+sin70°, ①
M-N=-cos40°+cos100°-sin30°
=-2sin70°sin30°-sin30°
=-sin70°-(1/2). ②
由①+②,得2M=(3/2).故M=(3/4).
4.(1)根据平移规律,得
C1:y-s=(x-t)3-(x-t).
(2)在曲线C上任取B1(x1,y1),设B2(x2,y2)是关于A的对称点,则(x1+x2/2)=(t/2),(y1+y2)/2=(s/2),所以x1=t-x2,y1=s-y2,代入C的方程,得s-y2=(t-x2)3-(t-x2),即y2-s=(x2-t)3-(x2-t),可知B2(x2,y2)在曲线C1上,同理C1上的点关于点A的对称点在曲线C上.因此,曲线C与C1关于点A对称.
5.(1)x1=(a/2),y1=(b/2).
(2)xn=a/(n+1),yn=(b/n+1).
(3)由Zn=xn·yn+1=a/(n+1)·b/(n+2)=(1/(n+1)-1/(n+2))ab,
得 Sn=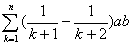 =((1/2)-1/(n+2))ab. =((1/2)-1/(n+2))ab. |
故 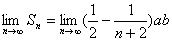 =(ab)/2. =(ab)/2. |
8.15.825英尺.
?§?4 怎样答高考开放性和情景性问题
1.C;2.B;3.D;4.(1/n).
5.在[0,+∞)上任取x1,x2,使0≤x1<x2,?
f(x1)-f(x2)
=(x12-x22)/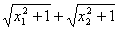 -a(x1-x2)
=(x1-x2)[((x1+x2)/
-a(x1-x2)
=(x1-x2)[((x1+x2)/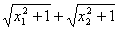 )-a].
∵x1-x2<0,0<((x1+x2/
)-a].
∵x1-x2<0,0<((x1+x2/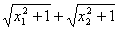 )<1,
(1)∴当a≥1时,f(x1)>f(x2),即f(x)在[0,+∞)上是增函数.
(2)当0<a<1时,f(x1)与f(x2)大小不确定.事实上,取x1=0,x2=2a/(1-a2), 则f(x1)=f(x2).
∴当0<a<1时,f(x)在[0,+∞)上不是单调函数.
∴a的取值范围是[1,+∞).
6.(1)由已知得2n+4=2+(n+2-1)d
)<1,
(1)∴当a≥1时,f(x1)>f(x2),即f(x)在[0,+∞)上是增函数.
(2)当0<a<1时,f(x1)与f(x2)大小不确定.事实上,取x1=0,x2=2a/(1-a2), 则f(x1)=f(x2).
∴当0<a<1时,f(x)在[0,+∞)上不是单调函数.
∴a的取值范围是[1,+∞).
6.(1)由已知得2n+4=2+(n+2-1)d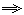 d=2.
∴ f(am)=2+(m+1-1)d=2m+2,
∴ logaam=2m+2,∴ am=a2m+2.
(2)bn=(2n+2)·a2n+2,
bn+1-bn=a2n+2[(2n+4)a2-(2n+2)].
令bn+1-bn>0,得a2>(n+1)/(n+2).∵ n∈N,a>0,a≠1,
∴ a>1.∴ a的取值范围是(1,+∞).
7.画图、观察、想象,猜测充要条件是矩形ABCD有一边平行于平面α.
d=2.
∴ f(am)=2+(m+1-1)d=2m+2,
∴ logaam=2m+2,∴ am=a2m+2.
(2)bn=(2n+2)·a2n+2,
bn+1-bn=a2n+2[(2n+4)a2-(2n+2)].
令bn+1-bn>0,得a2>(n+1)/(n+2).∵ n∈N,a>0,a≠1,
∴ a>1.∴ a的取值范围是(1,+∞).
7.画图、观察、想象,猜测充要条件是矩形ABCD有一边平行于平面α.
 |
|
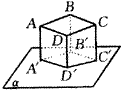
第7题 |
如图,四边形ABCD是矩形,AA′、BB′、CC′、DD′与α垂直,垂足分别为A′、B′、C′、D′,四边形A′B′C′D′是矩形的充要条件是矩形ABCD中有一条边平行于平面α.证之如下:(1)先证A′B′C′D′是平行四边形.∵BB′⊥α,CC′⊥α,∴BB′∥CC′.?∵ ABCD?是矩形,∴ AB∥CD,?∴ CC′、CD都平行于平面ABB′A′,?∴ 平面?DCC′D′∥平面ABB′A′.平面α与此两平面的交线分别为C′D′、A′B′,?∴ C′D′∥A′B′.同理B′C′∥A′D′,?∴ 四边形?A′B′C′D′是平行四边形.(2)当矩形ABCD中有边平行于α时,不妨设AB∥α.
∵ AA′⊥α,BB′⊥α,∴ AA′∥BB′, ∴ AA′B′B是平面四边形.∵ AB∥α,∴ AB∥A′B′,∴ AB⊥BB′.又AB⊥BC,∴ AB⊥平面BB′C′C.?∴ A′B′⊥平面BB′C′C. ∵ B′C′ 平面BB′C′C,?∴ A′B′⊥B′C′,?∴ A′B′C′D′是矩形;若A′B′C′D′是矩形,则∠A′B′C′=90°,∴ B′C′⊥A′B′,又B′C′⊥BB′,∴ B′C′⊥平面AA′B′B,∴ AB⊥B′C′.又AB⊥BC,若BC∥B′C′,BC
平面BB′C′C,?∴ A′B′⊥B′C′,?∴ A′B′C′D′是矩形;若A′B′C′D′是矩形,则∠A′B′C′=90°,∴ B′C′⊥A′B′,又B′C′⊥BB′,∴ B′C′⊥平面AA′B′B,∴ AB⊥B′C′.又AB⊥BC,若BC∥B′C′,BC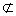 α,∴ BC∥α?,则必要性已证;若B′C′与BC不平行则相交,∴ AB⊥平面BB′C′C,∴ AB⊥BB′.又?A′B′⊥BB′,∴ AB∥A′B′.∵ AB
α,∴ BC∥α?,则必要性已证;若B′C′与BC不平行则相交,∴ AB⊥平面BB′C′C,∴ AB⊥BB′.又?A′B′⊥BB′,∴ AB∥A′B′.∵ AB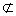 α,∴ AB∥α,?∴ 矩形ABCD总有一边所在直线与α平行.
∴ A′B′C′D′是矩形的充要条件是矩形ABCD的一边所在直线与α平行.
8.(1)设{an}的公差为d,则a2=a1+d=8,前10项之和为10a1+45d=185,解之得a1=5,d=3.?∴ an=3n+2,∴ bn=a2n=6·2n-1+2,∴ Sn=6·2n+2n-6.
(2)Tn=n(11+3n)=3n2+11n.对n=1,2,3,4,5分别求Sn、Tn的值,发现当1≤n≤3?时,Sn<Tn,当n=4或5时,Sn>Tn(数据略).猜想当n≥4时,Sn>Tn.?用数学归纳法证明如下:1°当n=4时,Sn=98,Tn=92,??∴ Sn>Tn成立.2°假设当n=k(k≥4)时Sn>Tn,?即6·2k+2k-6>3k2+11k,即6·2k>3k2+9k+6,
∴ 6·2k+1>6k2+18k+12=3(k+1)2+11(k+1)+3k2+k-2,∴ 6·2k+1+2(k+1)-6>3(k+1)2+11(k+1)+3k2+3k-6=3(k+1)2+11(k+1)+3(k+2)(k-1)>3(k+1)2+11(k+1).∴ 当n=k+1时,Sk+1>Tk+1也成立,∴ 当1≤n≤3时,Sn<Tn;?当n≥4时,Sn>Tn.
9.“用料最省”实际上等价于“无盖水箱表面积最小”.因此,设长方体水箱的长、宽、高分别是a、b、c,则abc=500.因S=2bc+2ac+ab≥3
α,∴ AB∥α,?∴ 矩形ABCD总有一边所在直线与α平行.
∴ A′B′C′D′是矩形的充要条件是矩形ABCD的一边所在直线与α平行.
8.(1)设{an}的公差为d,则a2=a1+d=8,前10项之和为10a1+45d=185,解之得a1=5,d=3.?∴ an=3n+2,∴ bn=a2n=6·2n-1+2,∴ Sn=6·2n+2n-6.
(2)Tn=n(11+3n)=3n2+11n.对n=1,2,3,4,5分别求Sn、Tn的值,发现当1≤n≤3?时,Sn<Tn,当n=4或5时,Sn>Tn(数据略).猜想当n≥4时,Sn>Tn.?用数学归纳法证明如下:1°当n=4时,Sn=98,Tn=92,??∴ Sn>Tn成立.2°假设当n=k(k≥4)时Sn>Tn,?即6·2k+2k-6>3k2+11k,即6·2k>3k2+9k+6,
∴ 6·2k+1>6k2+18k+12=3(k+1)2+11(k+1)+3k2+k-2,∴ 6·2k+1+2(k+1)-6>3(k+1)2+11(k+1)+3k2+3k-6=3(k+1)2+11(k+1)+3(k+2)(k-1)>3(k+1)2+11(k+1).∴ 当n=k+1时,Sk+1>Tk+1也成立,∴ 当1≤n≤3时,Sn<Tn;?当n≥4时,Sn>Tn.
9.“用料最省”实际上等价于“无盖水箱表面积最小”.因此,设长方体水箱的长、宽、高分别是a、b、c,则abc=500.因S=2bc+2ac+ab≥3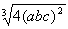 =300,
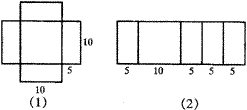
当且仅当2bc=2ac=ab,即a=b=10,c=5时,S达到最小值,故将此时的箱体展开成图(1),再拼成图(2),易知选择方案②最好.
=300,
当且仅当2bc=2ac=ab,即a=b=10,c=5时,S达到最小值,故将此时的箱体展开成图(1),再拼成图(2),易知选择方案②最好.
 |
|
第9题图 |
3.整体处理策略 整体处理,就是在处理问题时,利用问题中整体与部分的关系,通过整体代入、整体运算、整体消元、整体合并等方法,简化运算过程,提高解题速度,并从中感受到整体思维的和谐美. 例4?椭圆(x2/16)+(y2/4)=1上有两点P、Q,O是原点,若OP、OQ的斜率之积为-(1/4), (1)求证|OP|2+|OQ|2为定值; (2)求PQ的中点M的轨迹方程. 讲解:我们给出两种解法. 解法1.(1)设P、Q两点的坐标分别为P(x1,y1)、Q(x2,y2). ∵ P、Q分别在椭圆上,且kOP·kOQ=-(1/4).
∴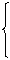 |
(x12/16)+(y12/4)=1, |
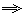 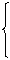 |
4y12=16-x12, |
① |
|
(x22/16)+(y22/4)=1, |
4y22=16-x22, |
② |
||
|
(y1/x1)·(y2/x2)=-(1/4) |
4y1y2=-x1x2. |
③ |
①×②,得 16y12y22=16?2-16(x12+x22)+x12x22. ④ ③代入④,得x12+x22=16. ①+②,得 y12+y22=8-(1/4)(x12+x22)=4.? ∴ |OP|2+|OQ|2=x12+y12+x22+y22=20.? (2)设P、Q的中点为M(x,y),则有 x1+x2=2x,y1+y2=2y. ①+②+③×2,得 4(y12+y22+2y1y2)=32-(x12+x22+2x1x2), ?∴ 4(y1+y2)2=32-(x1+x2)2, ∴ 4x2+16y2=32,即(x2/8)+(y2/2)=1. 故PQ的中点M的轨迹方程为(x2/8)+(y2/2)=1. 解法2.(1)设PQ的方程为y=mx+n(假设PQ的斜率存在),
由 |
x2+4y2=16, |
可得 |
|
y=mx+n |
x2+4y2=16((y-mx)/n)2, 令k=(y/x),上式可整理成 (16-4n2)k2-32mk+16m2-n2=0. 依题意,得k1k2=(16m2-n2)/(16-4n2)=-(1/4), 即8m2-n2+2=0.
又由 |
x2+4y2=16, |
可得 |
|
y=mx+n |
(1+4m2)x2+8mnx+4n2-16=0. 根据根与系数的关系得 x1+x2=-(8mn)/(1+4m2), x1·x2=(4n2-16)/(1+4m2). ∵ 8m2-n2+2=0,∴ 1+4m2=(1/2)n2, ∴ x1+x2=-(16m/n),x1·x2=(8(n2-4)/n2). ∴ |OP|2+|OQ|2=x12+(mx1+n)2+x22+(mx2+n)2 =(1+m2)(x12+x22)+2mn(x1+x2)+2n2 =(1+m2)[(x1+x2)2-2x1x2]+2mn(x1+x2)+2n2, 将韦达定理代入,可得(注意:n2=8m2+2)|OP|2+|OQ|2=20. (2)根据中点坐标公式可得
 |
2x0=x1+x2=-(16m/n), |
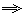  |
m=(x0y0)/(x02-8), |
|
y0=mx0+n |
n=8y0/(8-x02). |
代入8m2-n2+2=0,得
8(x02y02/(x02-8)2)-(64y02/(x02-8)2)+2=0.
整理,得x02+4y02=8,这就是所求的轨迹方程.
注:当PQ的斜率不存在时,容易讨论,这里略去.
4.联想迁移策略
联想是一种特定的想象.它是把某一领域的事物与其他领域的事物联系起来思考并由此激发新的认识的思维方式.数学解题需要联想.联想思维的过程实质上是一个知识迁移的过程.联想的目的是为了寻求解题途径,促使问题的解决,或归纳出一个比较理想的结论.
例5 已知i、m、n是正整数,且1<i≤m<n.
(Ⅰ)证明niPim<miPin;
(Ⅱ)证明(1+m)n>(1+n)m.
讲解:本题是2001年的高考题,难度较大,下面给出(Ⅱ)的不同于标准答案的三种证明方法.
方法1.设f(n)=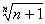 (n≥2),依题意只需证明函数f(n)递减,即当n≥3时,只需证明
(n≥2),依题意只需证明函数f(n)递减,即当n≥3时,只需证明
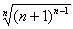 < <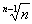 . . |
∵ 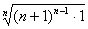 |
<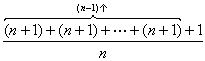 |
=((n-1)(n+1)+1/n)=n,
∴ 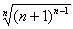 <n.
∴
<n.
∴ 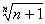 <
<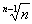 ,函数f(n)递减.
由m<n
,函数f(n)递减.
由m<n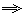 f(m)>f(n)
f(m)>f(n)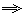
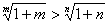
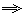 (1+m)n>(1+n)m.
方法2.设φ(x)=(ln(x+1)/x),下面证明φ(x)在[2,+∞)上单调递减.
∵ φ′(x)=((x/x+1)-ln(x+1)/x2),
又∵ (x/x+1)<1,x+1≥3>e,
∴ ?ln(x+1)>1,
即φ′(x)<0,
∴ φ(x)在[2,+∞)上递减.
∵ n>m≥2,
∴ φ(m)>φ(n),
∴ (ln(1+m)/m)>(ln(1+n)/n).
整理,得(1+m)n>(1+n)m.
方法3.先证明当n≥3时,xn=nn+1-(n+1)n>0.
显然x3=17>0,并且
xn+1=(n+1)n+2-(n+2)n+1?
=(n+2)n+1[(n+1)((n+1)/n+2))n+1-1].
∵ (n+1)/(n+2)>n/(n+1),
∴ xn+1>(n+2)n+1[(n+1)(n/(n+1))n+1-1]?
=(n+2)n+1(nn+1-(n+1)n/(n+1)n)
=((n+2)n+1/(n+1)n)xn>xn.
这说明数列{xn}是递增数列.
∴ xn>x3>0,
可得数列{
(1+m)n>(1+n)m.
方法2.设φ(x)=(ln(x+1)/x),下面证明φ(x)在[2,+∞)上单调递减.
∵ φ′(x)=((x/x+1)-ln(x+1)/x2),
又∵ (x/x+1)<1,x+1≥3>e,
∴ ?ln(x+1)>1,
即φ′(x)<0,
∴ φ(x)在[2,+∞)上递减.
∵ n>m≥2,
∴ φ(m)>φ(n),
∴ (ln(1+m)/m)>(ln(1+n)/n).
整理,得(1+m)n>(1+n)m.
方法3.先证明当n≥3时,xn=nn+1-(n+1)n>0.
显然x3=17>0,并且
xn+1=(n+1)n+2-(n+2)n+1?
=(n+2)n+1[(n+1)((n+1)/n+2))n+1-1].
∵ (n+1)/(n+2)>n/(n+1),
∴ xn+1>(n+2)n+1[(n+1)(n/(n+1))n+1-1]?
=(n+2)n+1(nn+1-(n+1)n/(n+1)n)
=((n+2)n+1/(n+1)n)xn>xn.
这说明数列{xn}是递增数列.
∴ xn>x3>0,
可得数列{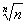 }递减.
(i)当n>m≥3时,有
}递减.
(i)当n>m≥3时,有
 >
>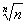 ,
即(1+m)n>nn+1.
∵ n>m≥3,
∴ (1+(1/n))m<(1+(1/n))n<3<n,
即nm+1>(1+n)m.
故(1+m)n>(1+n)m.
(ii)当m=2时,欲证不等式转化成
3n>(n+1)2.
该不等式极易用数学归纳法完成.
综合(i)、(ii),总有(1+m)n>(1+n)m成立.
5?分类讨论策略
分类讨论是一种“化整为零,各个击破”的思想方法.先根据题目要求确定适当的分类标准,然后对划分的每一类分别求解,如有必要可再加以分类,最后进行综合,从而得出结果.
例6?题目同例3
讲解:原不等式等价于不等式组
,
即(1+m)n>nn+1.
∵ n>m≥3,
∴ (1+(1/n))m<(1+(1/n))n<3<n,
即nm+1>(1+n)m.
故(1+m)n>(1+n)m.
(ii)当m=2时,欲证不等式转化成
3n>(n+1)2.
该不等式极易用数学归纳法完成.
综合(i)、(ii),总有(1+m)n>(1+n)m成立.
5?分类讨论策略
分类讨论是一种“化整为零,各个击破”的思想方法.先根据题目要求确定适当的分类标准,然后对划分的每一类分别求解,如有必要可再加以分类,最后进行综合,从而得出结果.
例6?题目同例3
讲解:原不等式等价于不等式组
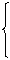 |
x-2>0, |
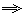 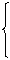 |
x>2, |
|
(x-4)a+4>0, |
x>4-(4/a), |
||
|
(x-2)2>(x-4)a+4 |
(x-a)(x-4)>0. |
由2=4-(4/a)得a=2,因此对a可分成以下几类:
①当1<a<2时,
4>4-(4/a)>2>a,
∴ x>4;
②当a=2时,可得x>4.
③当2<a<4时,
4>a>4-(4/a)>2,
∴ x>4或4-(4/a)<x<a;
④当a=4时,
∴ x>3且x≠4;
⑤当a>4时,
a>4>4-(4/a)>2,
∴ x>a或4-(4/a)<x<4.
综上可知:当1<a≤2时,x∈(4,+∞),当2<a≤4时,x∈(4-(4/a),a)∪(4,+∞),当a>4时,x∈(4-(4/a),4)∪(a,+∞).
三、专题训练
1?西部某地区因交通问题严重制约经济发展.某种土特产品只能在本地销售,每年投资x万元,所获利润为p=-(1/160)(x-40)2+10万元.在实施西部大开发战略中,该地区在制定经济发展十年规划时,拟开发此种土特产品.开发前后,财政预算每年均可投入专项资金60万元.要开发此产品,需先用5年时间修通公路,所需资金需从60万元的预算资金中每年拿出30万元.公路修通后该土特产品在异地销售,每投资x万元,可获利润q=-(159/160)(60-x)2+(119/2)(60-x)万元.问:从10年的总利润来看,该项目有无开发价值?
2?设函数f(x)=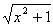 -ax,其中a>0.
(1)解不等式f(x)≤1;
(2)求a的取值范围,使函数f(x)在区间[0,+∞)上是单调函数.
3?求sin220°+cos250°+sin20°cos50°的值.
4?设曲线C的方程是y=x3-x,将C沿x轴、y轴正方向分别平移t、s个单位得曲线C1.
(1)写出曲线C1的方程;
(2)证明曲线C和C1关于点A((t/2),(s/2))对称.
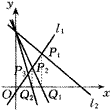
5?设a,b∈R+,直线l1:y=-(b/a)x+b与l2:y=(b/a)x的交点为P1(x1,y1),作点P1在x轴上的射影Q1(x1,0),过点A(0,b)与点Q1(x1,0)的直线AQ1交直线l2于P2(x2,y2);作点P2在x轴的射影Q2(x2,0),连直线AQ2交直线l2于P3(x3,y3),…,如此类推可得P1(x1,y1),P2(x2,y2),P3(x3,y3),…,Pn(xn,yn),…如图9-32.
-ax,其中a>0.
(1)解不等式f(x)≤1;
(2)求a的取值范围,使函数f(x)在区间[0,+∞)上是单调函数.
3?求sin220°+cos250°+sin20°cos50°的值.
4?设曲线C的方程是y=x3-x,将C沿x轴、y轴正方向分别平移t、s个单位得曲线C1.
(1)写出曲线C1的方程;
(2)证明曲线C和C1关于点A((t/2),(s/2))对称.
5?设a,b∈R+,直线l1:y=-(b/a)x+b与l2:y=(b/a)x的交点为P1(x1,y1),作点P1在x轴上的射影Q1(x1,0),过点A(0,b)与点Q1(x1,0)的直线AQ1交直线l2于P2(x2,y2);作点P2在x轴的射影Q2(x2,0),连直线AQ2交直线l2于P3(x3,y3),…,如此类推可得P1(x1,y1),P2(x2,y2),P3(x3,y3),…,Pn(xn,yn),…如图9-32.
 |
|
图9-32 |
(1)求x1,y1;
(2)求数列{xn},{yn}的通项;
(3)设zn=xn·yn+1,求数列{zn}的前n项和Sn,并求极限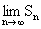 .
6?设关于x的一元二次方程2x2-ax-2=0的两个根为α、β(α<β),函数f(x)=(4x-a)/(x2+1).
(Ⅰ)求f(α)·f(β)的值;
(Ⅱ)证明f(x)在[α,β]上递增.
.
6?设关于x的一元二次方程2x2-ax-2=0的两个根为α、β(α<β),函数f(x)=(4x-a)/(x2+1).
(Ⅰ)求f(α)·f(β)的值;
(Ⅱ)证明f(x)在[α,β]上递增.
2.四棱锥P-ABCD中,底面四边形ABCD是正方形,侧面PCD是边长为a的正三角形,且平面PDC⊥底面ABCD,E为PC的中点。
(1)求异面直线PA与DE的距离。
 (2)求点D到平面PAB的距离。
(2)求点D到平面PAB的距离。
(1) D=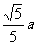
(1) D=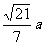
1.长方体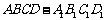 中,AB=
中,AB= ,BC=
,BC=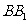 =1,E是BC的中点,F是CD的中点,
=1,E是BC的中点,F是CD的中点,
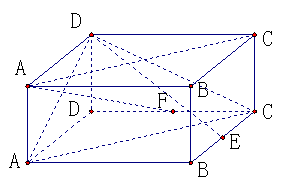 (1)求异面直线AF和
(1)求异面直线AF和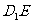 的距离。
的距离。
(2)求点B到平面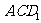 的距离。
的距离。
(3)求直线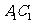 到平面
到平面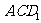 的距离。
的距离。
(1) D=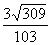
(2) D=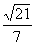
(3) D=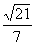
22.某房地产公司推出的售房有两套方案:一种是分期付款的方案,当年要求买房户首付3万元,然后从第二年起连续十年,每年付款8000元;另一种方案是一次性付款,优惠价为9万元,若一买房户有现金9万元可以用于购房,又考虑到另有一项投资年收益率为5%,他该采用哪种方案购房更合算?请说明理由.(参考数据1.059≈1.551,1.0510≈1.628)
21.已知数列 是等差数列,且
是等差数列,且
(1)求数列 的通项公式;
的通项公式;
(2)令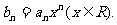 求数列
求数列 前n项和的公式.
前n项和的公式.
20.某渔业公司年初用98万元购买一艘捕鱼船,第一年各种费用12万元,以后每年都增加4万元,每年捕鱼收益50万元,
(1)问第几年开始获利?
(2)若干年后,有两种处理方案:
(3)年平均获利最大时,以26万元出售该渔船;
(4)总纯收入获利最大时,以8万元出售该渔船.
问哪种方案合算.
19.数列{an}满足a1=1,an=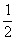 an-1+1(n≥2)
an-1+1(n≥2)
(1)若bn=an-2,求证{bn}为等比数列;
(2)求{an}的通项公式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com