
3.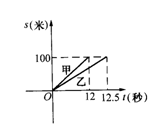 甲、乙二人在一次赛跑中,路程s与时间t的关系如图所示,从图中可以看出,下列结论错误的是( )
甲、乙二人在一次赛跑中,路程s与时间t的关系如图所示,从图中可以看出,下列结论错误的是( )
A.这是一次100米赛跑; B.甲比乙先到达终点
C.乙跑完全程需12.5秒; D.甲的速度是8米/秒
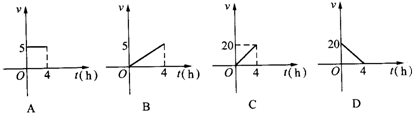
2.一根蜡烛原长20cm,点燃后每小时燃烧5cm,则燃烧的速度v(cm/h)与燃烧的时间t(h)的关系用图象表示为( )
1.如图是某市一天的气温随时间变化的图象,那么这天( )
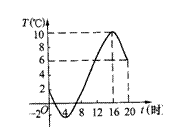 A.最高气温是10℃,最低气温是2℃;
A.最高气温是10℃,最低气温是2℃;
B.最高气温是6℃,最低气温是2℃
C.最高气温是10℃,最低气温是-2℃;
D.最高气温是6℃,最低气温是-2℃
21.解 : (1)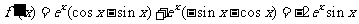 . ………………2分
. ………………2分
令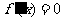 ,得
,得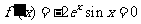 ,所以
,所以 ,
,
即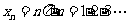
所以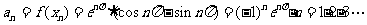 ………………4分
………………4分
所以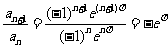 ,且
,且 ,
,
所以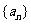 是以
是以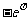 为首项,
为首项,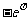 为公比的等比数列 .
………………6分
为公比的等比数列 .
………………6分
(2)由(1)知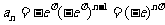 ,
,
所以 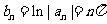 ,所以
,所以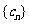 是以
是以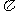 为首项,
为首项,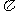 为公差等差数列, ………………8分
为公差等差数列, ………………8分
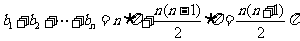 .
………………10分
.
………………10分
(3)
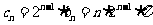 ,记数列
,记数列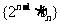 的前
的前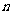 项的和为
项的和为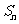 ,则
,则
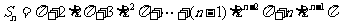 ,
………………11分
,
………………11分
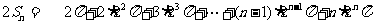 ,
,
两式相减得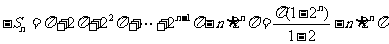 , …………13分
, …………13分
所以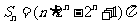 .
………………14分
.
………………14分
20.解: (1) 设椭圆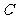 的半焦距为
的半焦距为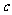 ,则
,则
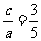 ,即
,即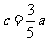 ① ,
………………1分
① ,
………………1分
又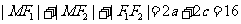 ② ,
………………2分
② ,
………………2分
联立①②,解得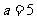 ,
,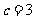 ,所以
,所以 ,
……………… 4分
,
……………… 4分
所以椭圆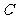 的方程为
的方程为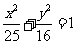 ;
………………6分
;
………………6分
而椭圆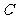 上点
上点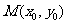 与椭圆中心
与椭圆中心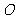 的距离为
的距离为
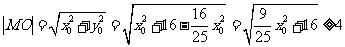 ,等号在
,等号在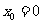 时成立, …………7分
时成立, …………7分
而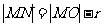 ,则
,则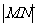 的最小值为
的最小值为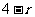 ,从而
,从而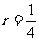 ,
,
则圆 的方程为
的方程为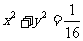 .
……………………8分
.
……………………8分
(2)因为点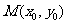 在椭圆
在椭圆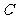 上运动,所以
上运动,所以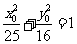 ,
,
即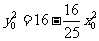 ,
…………………9分
,
…………………9分
圆心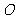 到直线
到直线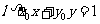 的距离
的距离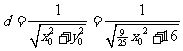 , ………………10分
, ………………10分
当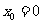 ,
,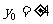 ,
,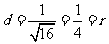 ,则直线
,则直线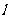 与圆
与圆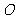 相切. ……………… 12分
相切. ……………… 12分
当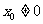 时,
时,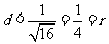 ,则直线
,则直线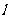 与圆
与圆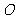 相交.
………………14分
相交.
………………14分
本题第1问直接指出点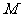 为椭圆短轴端点时
为椭圆短轴端点时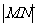 最小者要扣1分.
最小者要扣1分.
19.解:(1)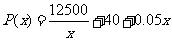 ,
……………2分
,
……………2分
由基本不等式得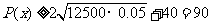 , ……………4分
, ……………4分
当且仅当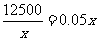 ,即
,即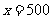 时,等号成立 , …………6分
时,等号成立 , …………6分
∴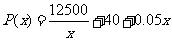 ,成本的最小值为
,成本的最小值为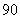 元. ………7分
元. ………7分
(2)设总利润为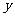 元,则
元,则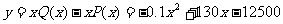
…………9分
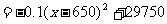 ,
………………10分
,
………………10分
当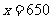 时,
时,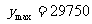 .
………………11分
.
………………11分
答:生产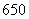 件产品时,总利润最高,最高总利润为
件产品时,总利润最高,最高总利润为 元. ………………12分
元. ………………12分
18.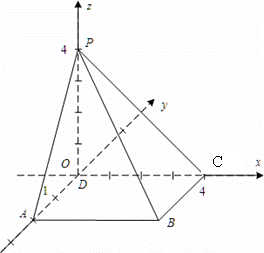 解: (1)直观图如图所示.
……………4分
解: (1)直观图如图所示.
……………4分
(2)由三视图得,底面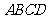 为正方形,
为正方形,
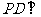 底面
底面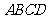 ,
,
则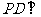
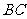 ,
,
而底面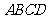 为正方形,
为正方形,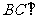
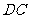 ,
,
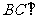 平面
平面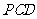 ,
,
从而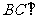
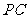 ;
;
同理,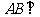
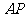 ,
,
因此,四个侧面都是直角三角形, …………6分
即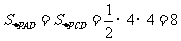 ,
,
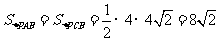 .
.
所以,几何体的表面积为 .
…………8分
.
…………8分
(3)设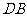 与
与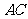 相交于点
相交于点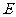 ,在
,在
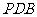 中,作
中,作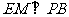 于
于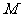 , …………9分
, …………9分
∵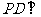 面
面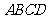 ,则
,则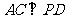 ,
,
由于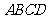 为正方形,则
为正方形,则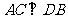 ,
,
∴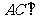 平面
平面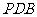 .
…………10分
.
…………10分
∴ 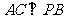 .
…………11分
.
…………11分
又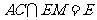 ,
,
则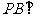 平面
平面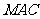 ,
…………12分
,
…………12分
在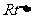
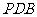 中,
中,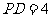 ,
,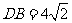 ,
,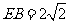 ,
,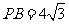 ,
,
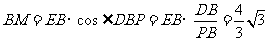 ,
,
则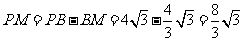 ,
…………13分
,
…………13分
故线段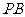 上是否存在点
上是否存在点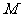 ,使得
,使得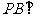 平面
平面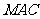 ,且
,且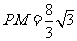 . ………14分
. ………14分
说明:未画虚线或长度不准确请酌情扣1-2分 .
17.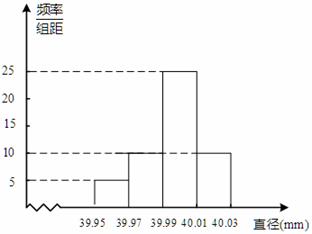 解 : (1)频率分布表如下……(3分 )
解 : (1)频率分布表如下……(3分 )
|
分组 |
频数 |
频率 |
 |
 |
10 |
0.10 |
5 |
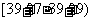 |
20 |
0.20 |
10 |
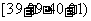 |
50 |
0.50 |
25 |
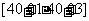 |
20 |
0.20 |
10 |
|
合计 |
100 |
1 |
|
频率分布直方图如图 ………………6分
(2)误差不超过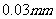 ,即直径落在
,即直径落在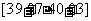 范围内的概率为
范围内的概率为
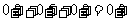 .
……………9分
.
……………9分
(3)整体数据的平均值约为
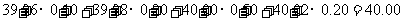 (
( ).
…………13分
).
…………13分
注:频率分布表可不要最后一列,这里列出,只是为画频率分布图方便.
16.((1)解:(1)由于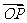
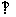
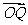 ,则
,则 , ………………3分
, ………………3分
显然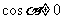 ,两边同时除以
,两边同时除以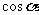 得,
得,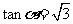 ;
………………6分
;
………………6分
(2)由于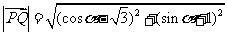 ,
………………8分
,
………………8分
即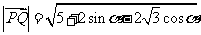 ,
,
∴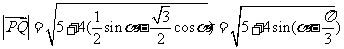 ………………10分
………………10分
由于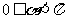 ,则
,则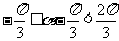 ,
………………11分
,
………………11分
则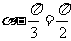 ,即
,即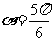 时,
时,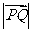 最大值为
最大值为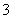 .
………………13分
.
………………13分
说明:本题第(1)问可以利用解析几何两直线垂直的条件求出,第(2)问可以结合平面几何知识得出.
(二)选做题(14-15题,考生只能从中选做一题)
14. 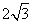 .解析:将其化为直角坐标方程为
.解析:将其化为直角坐标方程为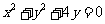 ,和
,和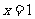 ,代入得:
,代入得: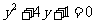
则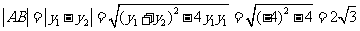 .
.
15. 15.解析:由三角形相似可得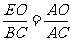 ,解得
,解得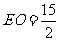 ,由对称性知
,由对称性知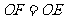 ,所以
,所以 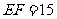 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com