
1.
已知集合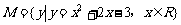 ,集合
,集合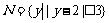 ,则
,则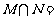 ( )
( )
A.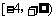 B.
B.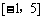 C.
C.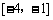 D.
D.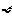

22、解:(Ⅰ)因为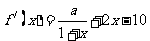 ,
,
所以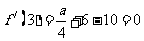 ,因此
,因此 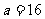 …………4分
…………4分
(Ⅱ)由(Ⅰ)知,
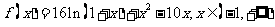 ,
,
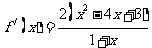 .
………………5分
.
………………5分
当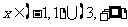 时,
时,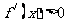 , ………………6分
, ………………6分
当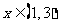 时,
时,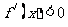 . ………………7分
. ………………7分 

所以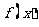 的单调增区间是
的单调增区间是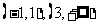 ,
,
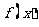 的单调减区间是
的单调减区间是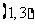 .
………………8分
.
………………8分
(Ⅲ)由(Ⅱ)知,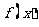 在
在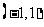 内单调增加,在
内单调增加,在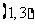 内单调减少,在
内单调减少,在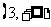 上单调增加,且当
上单调增加,且当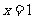 或
或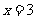 时,
时,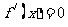 , ………………9分
, ………………9分
所以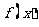 的极大值为
的极大值为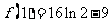 ,极小值为
,极小值为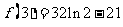 . ……10分
. ……10分
因此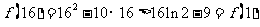 ,
,
 , ………………12分
, ………………12分
所以在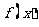 的三个单调区间
的三个单调区间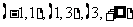 直线
直线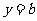 有
有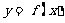 的图象各有一个交点,当且仅当
的图象各有一个交点,当且仅当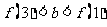 ,
,
因此,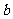 的取值范围为
的取值范围为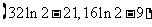 . ………………14分
. ………………14分 

21、解:(1)设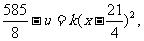
∵售价为10元时,年销量为28万件;
∴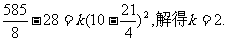
∴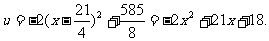
∴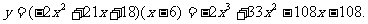 …………6分
…………6分
(2)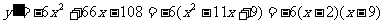
令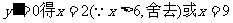
显然,当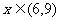 时,
时,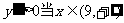 时,
时,
∴函数 上是关于x的增函数;
上是关于x的增函数;
在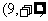 上是关于x的减函数。……………………10分
上是关于x的减函数。……………………10分 

∴当x=9时,y取最大值,且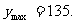
∴售价为9元时,年利润最大,最大年利润为135万元。………………12分
20、解:(1)令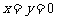 ,得
,得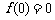
令 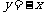 ,得
,得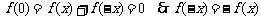 所以函数
所以函数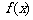 为奇函数。
为奇函数。
(2)在R上任取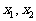 ,且
,且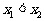 ,则
,则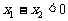 ,所以
,所以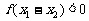
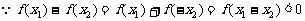
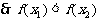 所以函数
所以函数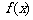 为增函数。
为增函数。
(3)由(2)得函数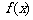 为增函数,
为增函数,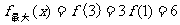
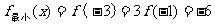
19、⑴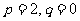 ⑵略
⑵略 

18、解:由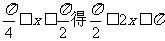
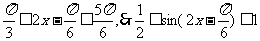 ,
,
即 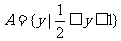 ………………4分
………………4分
∴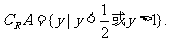 …………5分
…………5分
又关于x的方程 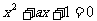 的根一个在(0,1)上,另一个在(1,2)上,设函数
的根一个在(0,1)上,另一个在(1,2)上,设函数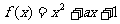 ,则满足
,则满足
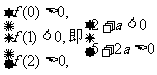 , ∴
, ∴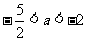 ………………9分
………………9分
∴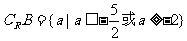 ………………10分
………………10分
∴ …………12分
…………12分
17、解:(1)由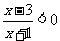 ,得
,得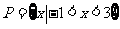 .
.
(2)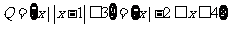 .
.
当 时,得
时,得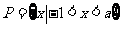 ,又
,又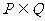 ,所以
,所以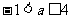 ,
,
当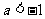 时,得
时,得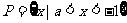 ,又
,又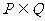 ,所以
,所以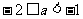 ,
,
当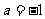 时,得
时,得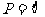 ,满足
,满足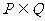 ,所以,
,所以,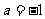 符合题意。
符合题意。
综上,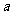 的取值范围是
的取值范围是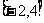 .
. 

13、3 14、 15、3 16、①②③④
22、(本题14分)已知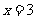 是函数
是函数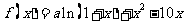 的一个极值点。
的一个极值点。
⑴求实数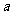 的值;
的值;
⑵求函数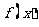 的单调区间;
的单调区间; 

⑶若直线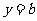 与函数
与函数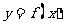 的图象有3个交点,求
的图象有3个交点,求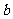 的取值范围.
的取值范围.
21、(本题12分)某种产品每件成本为6元,每件售价为x元(x>6),年销量为u万件,若已知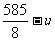 与
与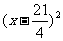 成正比,且售价为10元时,年销量为28万件。
成正比,且售价为10元时,年销量为28万件。
⑴求年销售利润y关于x的函数关系式; 

⑵求售价为多少时,年利润最大,并求出最大年利润。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com