
21.(本题满分14分)
已知数列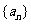 中,
中,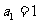 ,且
,且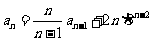
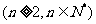 .
.
(Ⅰ) 求数列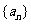 的通项公式;
的通项公式;
(Ⅱ) 令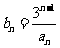
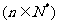 ,数列
,数列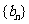 的前
的前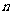 项和为
项和为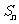 ,试比较
,试比较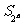 与
与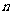 的大小;
的大小;
(Ⅲ) 令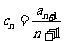
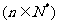 ,数列
,数列 的前
的前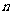 项和为
项和为 .求证:对任意
.求证:对任意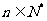 ,
,
都有  .
.
21解:(Ⅰ)由题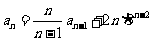 知,
知, 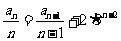 ,
,
由累加法,当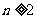 时,
时,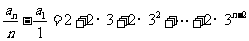
代入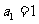 ,得
,得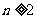 时,
时,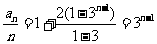
又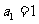 ,故
,故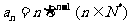 .
................4分
.
................4分
(II)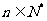 时,
时,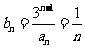 .
.
方法1:当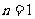 时,
时,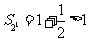 ;当
;当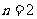 时,
时,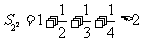 ;
;
当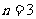 时,
时,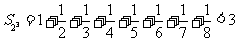 .
.
猜想当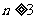 时,
时,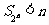 .
................6分
.
................6分
下面用数学归纳法证明:
①当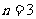 时,由上可知
时,由上可知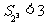 成立;
成立;
②假设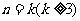 时,上式成立,即
时,上式成立,即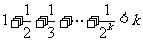 .
.
当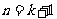 时,左边
时,左边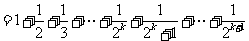
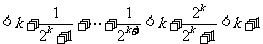 ,所以当
,所以当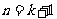 时成立.
时成立.

 由①②可知当
由①②可知当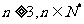 时,
时,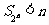 .
.
综上所述:当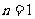 时,
时,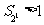 ;当
;当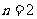 时,
时,  ;
;
当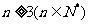 时,
时,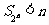 .
...............10分
.
...............10分
方法2: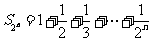
记函数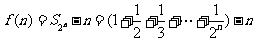
所以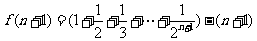 .........6分
.........6分
则
所以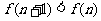 .
.
由于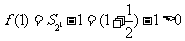 ,此时
,此时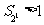 ;
;
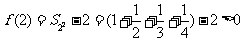 ,此时
,此时 ;
;
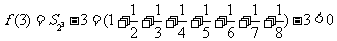 ,此时
,此时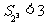 ;
;
由于,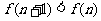 ,故
,故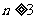 时,
时,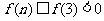 ,此时
,此时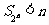 .
.
综上所述:当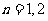 时,
时,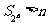 ;当
;当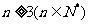 时,
时,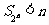 . ...........10分
. ...........10分
(III)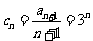
当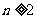 时,
时,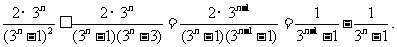
所以当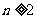 时
时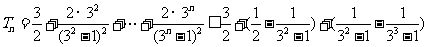
+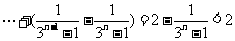 .
.
且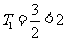
故对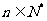 ,
, 得证.
.................14分
得证.
.................14分
20.(本题满分13分)
已知函数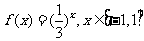 ,函数
,函数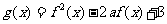 的最小值为
的最小值为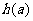 .
.
(1)求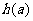 的解析式;
的解析式;
(2)是否存在实数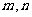 同时满足下列两个条件:①
同时满足下列两个条件:①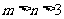 ;②当
;②当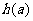 的定义域为
的定义域为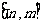 时,值域为
时,值域为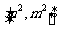 ?若存在,求出
?若存在,求出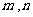 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
20解:(1)由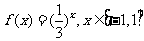 ,知
,知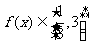 ,令
,令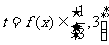
............1分
记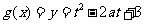 ,则
,则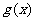 的对称轴为
的对称轴为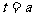 ,故有:
,故有:
①当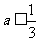 时,
时,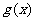 的最小值
的最小值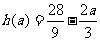
②当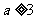 时,
时,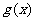 的最小值
的最小值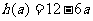
③当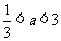 时,
时,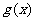 的最小值
的最小值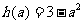
综述,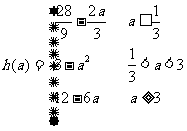 ............7分
............7分
(2)当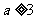 时,
时,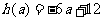 .故
.故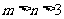 时,
时,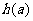 在
在 上为减函数.
上为减函数.
所以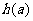 在
在 上的值域为
上的值域为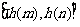 .
............9分
.
............9分
由题,则有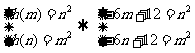 ,两式相减得
,两式相减得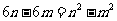 ,又
,又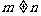
所以 ,这与
,这与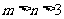 矛盾.故不存在满足题中条件的
矛盾.故不存在满足题中条件的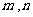 的值.
的值.
............13分
19.(本题满分12分)
已知二次函数 ,不等式
,不等式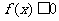 的解集有且只有一个元素,设数列
的解集有且只有一个元素,设数列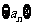 的前
的前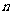 项和为
项和为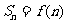 .
.
(1)求数列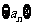 的通项公式;
的通项公式;
(2)设各项均不为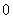 的数列
的数列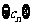 中,满足
中,满足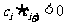 的正整数
的正整数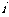 的个数称作数列
的个数称作数列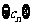 的变号数,令
的变号数,令 ,求数列
,求数列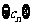 的变号数.
的变号数.
19解:(1)由于不等式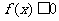 的解集有且只有一个元素,
的解集有且只有一个元素,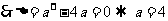
故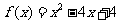 .
..................2分
.
..................2分
由题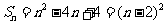
则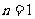 时,
时,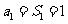 ;
;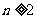 时,
时,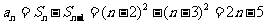
故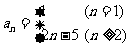 ...................6分
...................6分
(2)由题可得,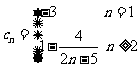
由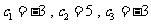 ,所以
,所以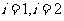 都满足
都满足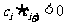 ..............8分
..............8分
当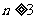 时,
时,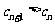 ,且
,且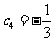 ,同时
,同时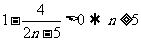 ,可知
,可知
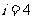 满足
满足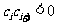 ;
;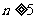 时,均有
时,均有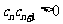 .
.
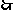 满足
满足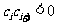 的正整数
的正整数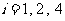 ,故数列
,故数列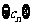 的变号数
的变号数 . ............12分
. ............12分
18.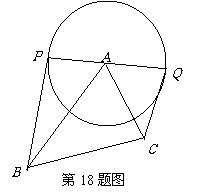 (本题满分12分)
(本题满分12分)
已知 中,
中,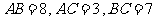 ,
,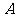 为圆心,直径
为圆心,直径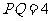 ,求
,求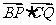 的最大值、最小值,并分别指出取得最值时
的最大值、最小值,并分别指出取得最值时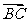 与
与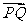 夹角的大小.
夹角的大小.
18解:在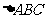 中,由余弦定理知
中,由余弦定理知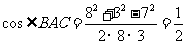 ,故
,故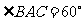 .
.
............3分
所以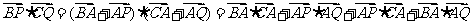
=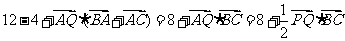 ..........7分
..........7分
故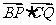 的最大值为
的最大值为 ,此时
,此时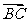 与
与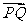 夹角为
夹角为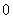 .
.
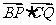 的最小值为
的最小值为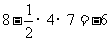 ,此时
,此时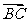 与
与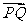 夹角为
夹角为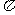 .
.........12分
.
.........12分
17.(本题满分12分)
已知函数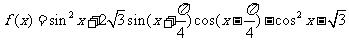 .
.
(1)求函数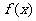 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)求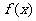 在
在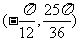 上的值域.
上的值域.
17解:(1)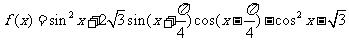
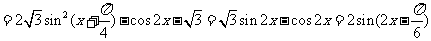
..............3分
故函数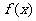 的最小正周期
的最小正周期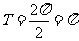
令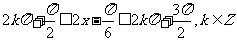 ,得
,得
故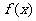 的单调递减区间为
的单调递减区间为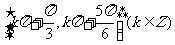 .
..............6分
.
..............6分
(2)当 ,知
,知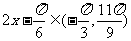 ,故
,故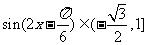 .
.
所以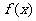 在
在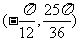 上的值域是
上的值域是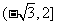 .
..............12分
.
..............12分
16.(本题满分12分)
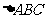
 中,角
中,角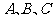 的对边分别为
的对边分别为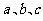 ,且
,且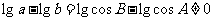 .
.
(1)判断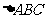 的形状;
的形状;
(2)设向量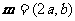 ,
,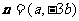 ,且
,且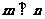 ,
, ,求
,求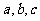 .
.
16解:(1)由题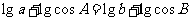 ,故
,故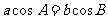 ,
,
由正弦定理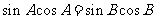 ,即
,即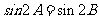 .
.
又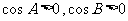 ,故
,故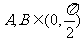 ,
,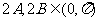
因 ,故
,故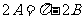 .
.
即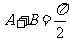 ,故
,故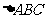 为直角三角形.
..............6分
为直角三角形.
..............6分
(2)由于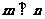 ,所以
,所以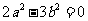 ①
①
且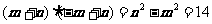 ,即
,即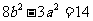 ②
②
联立①②解得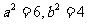 ,故在直角
,故在直角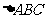 中,
中,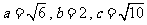 .......12分
.......12分
15.已知函数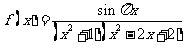 .
.
(Ⅰ)方程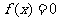 在区间
在区间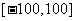 上实数解的个数是__________;
上实数解的个数是__________;
(Ⅱ)对于下列命题:① 函数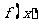 是周期函数;
是周期函数;
② 函数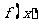 既有最大值又有最小值;
既有最大值又有最小值;
③ 函数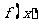 的定义域是R,且其图象有对称轴;
的定义域是R,且其图象有对称轴;
④对于任意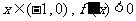 (
( 是函数
是函数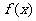 的导函数).
的导函数).
其中真命题的序号是 .(填写出所有真命题的序号)
15答案: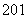 ;②③
;②③
解析:(Ⅰ)由于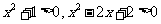 ,故
,故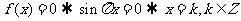
在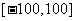 中的整数个数
中的整数个数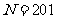
故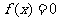 在区间
在区间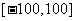 上实数解的个数为
上实数解的个数为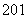 .
.
(Ⅱ)命题①:由分母为 ,易知
,易知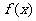 不是周期函数,故为假命题;
不是周期函数,故为假命题;
命题②:由于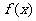 是
是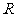 上的连续函数,且
上的连续函数,且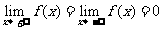 ,可知
,可知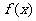 既有最大值又有最小值,故为真命题;
既有最大值又有最小值,故为真命题;
命题③:由于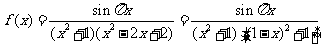 ,故
,故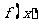 的定义域是R
的定义域是R
看到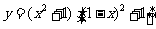 的对称轴为
的对称轴为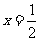 ,且
,且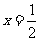 为
为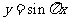 的一条对称轴
的一条对称轴
故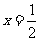 为
为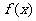 图象的对称轴,故为真命题;
图象的对称轴,故为真命题;
命题④:由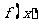 在定义域R上连续,且
在定义域R上连续,且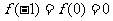 ,可知
,可知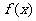 不可能在
不可能在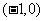 上为减函数,故为假命题.
上为减函数,故为假命题.
14.已知数列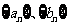 都是公差为
都是公差为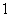 的等差数列,其首项分别为
的等差数列,其首项分别为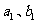 ,且
,且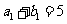 ,
,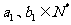 .设
.设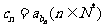 ,则数列
,则数列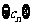 的前
的前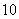 项和为
.
项和为
.
14答案: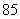
解析:设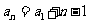 ,
,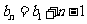 ,则
,则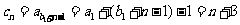 .
.
所以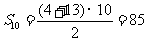 .
.
13.已知函数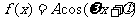 的图象如
的图象如
图所示,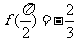 ,则
,则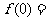 .
.
13答案:
解析:由图象可得最小正周期为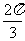 .
.
所以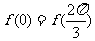 ,注意到
,注意到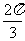 与
与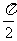 关于
关于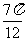 对称,故
对称,故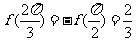 .
.
12.已知向量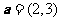 ,
,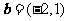 ,则
,则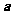 在
在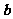 方向上的投影等于 .
方向上的投影等于 .
12答案: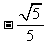
 解析:
解析: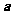 在
在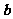 方向上的投影为
方向上的投影为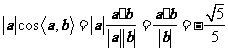 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com