
6.(2007全国Ⅰ)设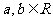 ,集合
,集合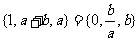 ,则
,则 ( C )
( C )
A.1
B.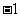 C.2
D.
C.2
D.
5. (2009广东理)已知全集
(2009广东理)已知全集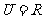 ,集合
,集合 和
和
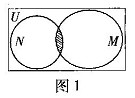
 的关系的韦恩(Venn)图如图1所示,则阴影部分所示的集合的元素共有 ( B )
的关系的韦恩(Venn)图如图1所示,则阴影部分所示的集合的元素共有 ( B )
A.3个 B.2个 C.1个 D. 无穷多个
4.(2009北京文)设集合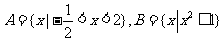 ,则
,则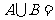 ( A )
( A )
A.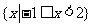 B.
B.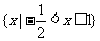 C.
C.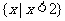 D.
D.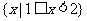
3.已知集合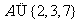 且
且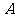 中至多有一个奇数,则这样的集合 ( A )
中至多有一个奇数,则这样的集合 ( A )
A.6个 B.5个 C.4个 D.2个
2.(2009山东文)集合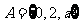 ,
,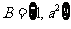 ,若
,若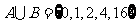 ,则
,则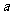 的值为( D )
的值为( D )
A.0 B.1 C.2 D.4
1.给出6个关系式:(1)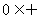 ,(2)
,(2)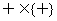 ,(3)
,(3)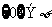 ,(4)
,(4)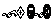 ,(5)
,(5)
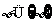 ,(6)
,(6)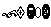 .其中正确的个数是 ( C )
.其中正确的个数是 ( C )
A.3 B.4 C. 5 D.6
4. 设集合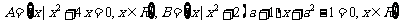 .
.
若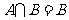 ,求实数
,求实数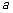 的取值范围.
的取值范围.
[解析]∵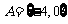 ,又
,又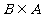 ,所以
,所以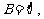 或
或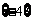 ,或
,或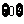 ,或
,或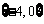 .
.
(1)当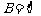 时,
时,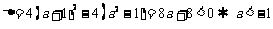 .
.
(2)当 时,
时,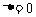 ,且
,且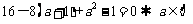 .
.
(3)当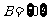 时,
时,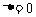 ,且
,且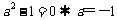 .
.
(4)当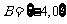 时,
时,
综上所述,实数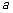 的取值范围是
的取值范围是 .
.
能力训练
3.(2009山东理)集合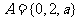 ,
,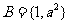 ,若
,若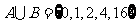 ,则
,则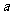 的值为( )
的值为( )
A.0 B.1 C.2 D.4
[解析]:∵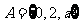 ,
,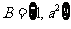 ,
,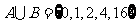 ∴
∴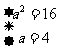 ∴
∴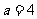 ,故选D.
,故选D.
答案:D
题型4 空集的考查
例4 已知集合A=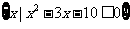 ,B=
,B=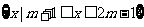 ,且
,且 , 则实数m的取值范围是( )
, 则实数m的取值范围是( )
A.  B.
B. 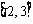 C.
C. 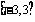 D.
D.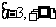
[解析]∵A=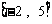 , 由
, 由 得:①
得:①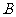 =Æ,则
=Æ,则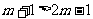 ,即
,即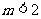 ;
;
②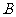 ≠Æ,则
≠Æ,则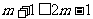 且
且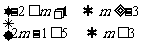
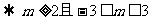 ,即
,即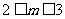 ,知
,知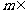
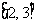 . 综上故选A.
. 综上故选A.
[点评] 解答具有条件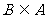 的试题时,不能忽略B=Æ的情形.空集是一个特殊的集合,在研究集合之间的关系与运算时必须注意.
的试题时,不能忽略B=Æ的情形.空集是一个特殊的集合,在研究集合之间的关系与运算时必须注意.
[变式与拓展]
2. (2009广东文)已知全集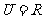 ,则正确表示集合
,则正确表示集合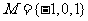 和
和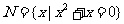 关系的韦恩(
关系的韦恩( )图是
)图是
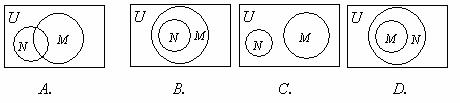
[解析]由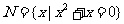 ,得
,得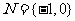 ,则
,则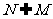 ,选B.
,选B.
题型3 集合间的基本关系
[例3]已知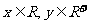 ,集合
,集合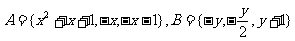 .若
.若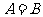 ,则
,则 的值是( )
的值是( )
A.5 B.4 C.25 D.10
[解析]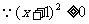 ,
,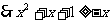 ,且
,且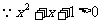 及集合中元素的互异性知
及集合中元素的互异性知
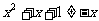 ,即
,即 ,此时应有
,此时应有 .
.
而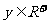 ,从而在集合B中,
,从而在集合B中,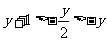 .
.
由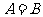 ,得
,得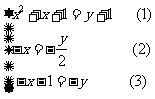
由(2)(3)解得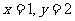 ,代入(1)式知
,代入(1)式知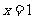 ,
,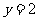 也满足(1)式,
也满足(1)式,
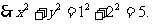
[点评]本题主要考查集合相等的的概念,如果两个集合中的元素个数相等,那么两个集合中对应的元素应分别相等才能保证两个集合相等.而找到这种对应关系往往是解决此类题目的关键.
设集合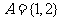 ,则满足
,则满足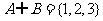 的集合B的个数是( )。
的集合B的个数是( )。
A.1 B.3 C.4 D.8
[解析]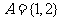 ,
,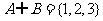 ,则集合B中必含有元素3,即此题可转化为求集合
,则集合B中必含有元素3,即此题可转化为求集合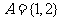 的子集个数问题,所以满足题目条件的集合B共有
的子集个数问题,所以满足题目条件的集合B共有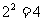 个.故选择答案C.
个.故选择答案C.
[点评] 集合A是n个元素的集合,则集合A有2n个子集、2n-1个真子集、2n-2个非空真子集.
[变式与拓展]
1.已知集合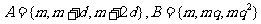 ,
,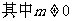 ,
,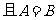 ,求
,求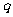 的值.
的值.
[解析]由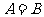 可知,
可知,
(1)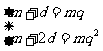 ,或(2)
,或(2)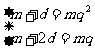
解(1)得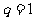 ,
,
解(2)得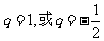 ,
,
又因为当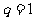 时,
时,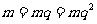 与题意不符,所以,
与题意不符,所以,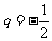 .
.
[题型2]集合的表示法
[例2]已知集合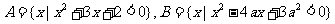 且
且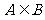 ,求参数
,求参数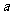 的取值范围.
的取值范围.
[解析]由已知易求得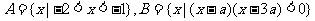
当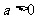 时,
时,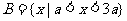 ,由
,由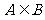 知无解;
知无解;
当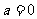 时,
时,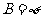 ,显然无解;
,显然无解;
当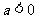 时,
时, 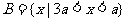 ,由
,由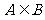 解得
解得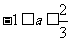 .
.
综上知,参数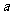 的取值范围是
的取值范围是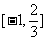 .
.
[点评]本题中,集合的定义是一个二次三项式,那么寻于集合B要分类讨论使其取值范围数字化,才能通过条件求出参数的取值范围.
[变式与拓展]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com