
21、(14分)在直角坐标平面上有一点列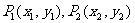 …
…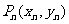 …,对一切正整数
…,对一切正整数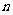 ,点
,点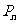 位于函数
位于函数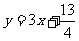 的图象上,且
的图象上,且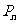 的横坐标构成以
的横坐标构成以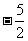 为首项,
为首项,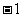 为公差的等差数列
为公差的等差数列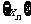 。⑴求点
。⑴求点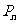 的坐标;⑵设抛物线列
的坐标;⑵设抛物线列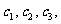 …
…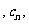 …中的每一条的对称轴都垂直于
…中的每一条的对称轴都垂直于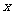 轴,第
轴,第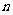 条抛物线
条抛物线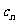 的顶点为
的顶点为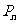 ,且过点
,且过点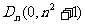 ,记与抛物线
,记与抛物线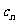 相切于
相切于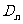 的直线的斜率为
的直线的斜率为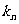 ,求:
,求: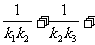 …
…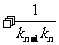 。
。
⑶设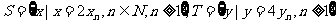 ,等差数列
,等差数列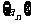 的任一项
的任一项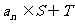 ,其中
,其中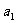 是
是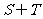 中的最大数,
中的最大数,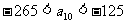 ,求
,求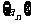 的通项公式。
的通项公式。
20、(13分)已知函数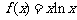 .
.
(Ⅰ)求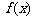 的最小值;
的最小值;
(Ⅱ)若对所有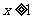 都有
都有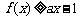 ,求实数
,求实数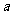 的取值范围.
的取值范围.
19、(12分)已知函数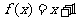 ,设
,设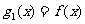 ,
,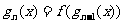
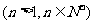
(1)求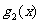 ,
,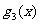 的表达式,并猜想
的表达式,并猜想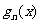
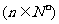 的表达式(直接写出猜想结果)
的表达式(直接写出猜想结果)
(2)求关于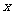 的二次函数
的二次函数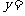
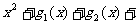 …
…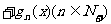 的最小值。
的最小值。
18、(12分)已知P:对任意 恒成立;
恒成立;
Q:函数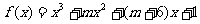 存在极大值和极小值。
存在极大值和极小值。
求使“P且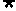 Q”为真命题的m的取值范围。
Q”为真命题的m的取值范围。
17、(12分)某大型企业人力资源部为了研究企业员工工作积极性和对待企业改革的关系,随机抽取了100名员工进行调查,其中支持企业改革的调查者中,工作积极的46人,工作一般的35人,而不太赞成企业改革的调查者中,工作积极的4人,工作一般的15人.
(1)
根据以上数据建立一个 的列联表;
的列联表;
(2)
对于人力资源部的研究 项目,根据以上数据可以认为企业的全体员工对待企业改革的态度与其工作积极性是否有关系?
项目,根据以上数据可以认为企业的全体员工对待企业改革的态度与其工作积极性是否有关系?
参考公式: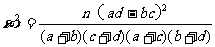 (其中
(其中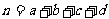 )
)
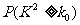 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
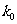 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
16、(12分) 已知复数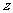 满足
满足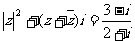 (
( i为虚数单位),求
i为虚数单位),求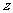 。
。
15.给出下列四个结论:
 ①
① 在画两个变量的散点图时,预报变量在
在画两个变量的散点图时,预报变量在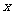 轴上,解释变量在
轴上,解释变量在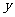 轴上;
轴上; 
②线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越小;
 ③用独立性检验(2Χ2列联表法)来考察两个分类变量是否有关系时,算出的随机变量k2的值越大,说明“x与y有关系”成立的可能性越大;
③用独立性检验(2Χ2列联表法)来考察两个分类变量是否有关系时,算出的随机变量k2的值越大,说明“x与y有关系”成立的可能性越大;
 ④残差平方和越小的模型,拟合的效果越好;
④残差平方和越小的模型,拟合的效果越好;
 其中
其中 结论正确的序号为
。(写出你认为正确的所有结论的序号)
结论正确的序号为
。(写出你认为正确的所有结论的序号)
14.已知两点等分单位圆时,有相应正确关系为: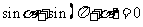 ;三点等分单位圆时,有相应正确关系为
;三点等分单位圆时,有相应正确关系为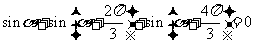 .由此可以推知四点等分单位圆时的相应正确关系:
。
.由此可以推知四点等分单位圆时的相应正确关系:
。
13.在数列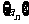 中,若对任意正整数
中,若对任意正整数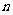 ,
,

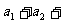 …
… 则
则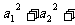 …
…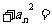 ___________________。
___________________。
12.对任意非零实数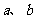 ,若
,若 的运算原理如右图所示,则
的运算原理如右图所示,则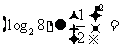 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com