
3. 利用函数的单调性,结合图象还可以看出:
(1)在[a,b]上,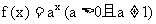 值域是
值域是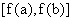 或
或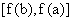 ;
;
(2)若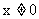 ,则
,则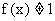 ;
;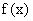 取遍所有正数当且仅当
取遍所有正数当且仅当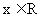 ;
;
(3)对于指数函数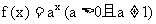 ,总有
,总有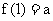 ;
;
(4)当 时,若
时,若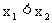 ,则
,则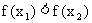 ;
;
例1、比较下列各组数的大小
(1)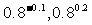 ; (2)
; (2)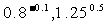 ; (3)
; (3)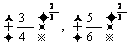
解:(1)因为函数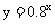 为单调减函数,且-0.1<0.2,所以
为单调减函数,且-0.1<0.2,所以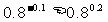 ;
;
(2)因为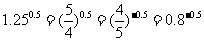 ,并且函数
,并且函数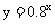 为单调减函数,又因为-0.5<-0.1<0,所以
为单调减函数,又因为-0.5<-0.1<0,所以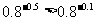 , 即
, 即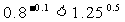 ;
;
(3)因为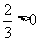 ,当
,当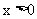 时,函数
时,函数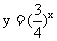 上的点在函数
上的点在函数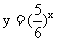 的下方,所以
的下方,所以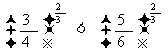 .
.
练习1.比较下列各题中两个值的大小:
(1) 1.72.5,1.73;
(2) 8-0.1,80.2;
(3) 1.70.3,0.93.1
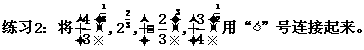
答案: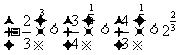
例2.设y1=a3x+1,y2=a-2x,其中a>0且a¹1,确定x为何值时,有
(1)y1=y2 (2)y1>y2
解:因为指数函数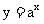 为单调函数,
为单调函数,
(1)当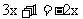 ,即
,即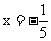 时,有y1=y2
时,有y1=y2
(2)当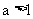 时, 指数函数
时, 指数函数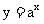 为单调增函数,
为单调增函数,
所以当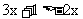 ,即
,即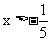 时,有y1>y2;
时,有y1>y2;
当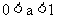 时, 指数函数
时, 指数函数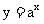 为单调减函数,
为单调减函数,
所以当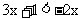 ,即
,即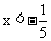 时,有y1>y2.
时,有y1>y2.
练习3.若指数函数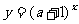 在
在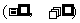 上是减函数,那么( )
上是减函数,那么( )
A.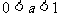 B.
B.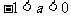 C.
C.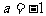 D.
D.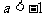
练习4.已知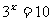 ,则这样的
,则这样的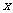 ( )
( )
A.存在且只有一个 B.存在且不只一个
C.存在且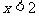 D.根本不存在
D.根本不存在
课本练习: 练习1. 1; 练习2. 1,2
课堂小结:1.比较两个指数的大小; 2.解简单的指数不等式
作业:习题3-3B组1-6
2.你能根据指数函数的图象的特征归纳出指数函数的性质吗?

|
图象特征 |
函数性质 |
||
 |
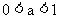 |
 |
 |
|
向x、y轴正负方向无限延伸 |
函数的定义域为R |
||
|
图象关于原点和y轴不对称 |
非奇非偶函数 |
||
|
函数图象都在x轴上方 |
函数的值域为R+ |
||
|
函数图象都过定点(0,1) |
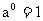 |
||
自左向右看,  图象逐渐上升 |
自左向右看, 图象逐渐下降 |
增函数 |
减函数 |
|
在第一象限内的图象纵坐标都大于1 |
在第一象限内的图象纵坐标都小于1 |
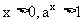 |
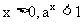 |
|
在第二象限内的图象纵坐标都小于1 |
在第二象限内的图象纵坐标都大于1 |
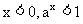 |
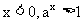 |
|
图象上升趋势是越来越陡 |
图象上升趋势是越来越缓 |
函数值开始增长较慢,到了某一值后增长速度极快; |
函数值开始减小极快,到了某一值后减小速度较慢; |
3、情感.态度与价值观

使学生通过学习指数函数的图像,了解到指数函数具有的性质.在学习的过程中体会研究具体函数及其性质的过程和方法,如具体到一般的过程、数形结合的方法等,增强学习指数函数的积极性和自信心.

[教学重点]: 指数函数的图像和性质.

[教学难点]:指数函数的图像和性质与底数的关系

[学法指导]:学生思考、探究.

[讲授过程]

[新课导入]

[互动过程1]

复习:指数函数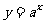 在底数
在底数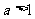 及
及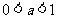 这两种情况下的图像和性质
这两种情况下的图像和性质

练习:1.在同一坐标系中画出下列函数的图象:

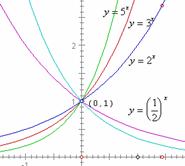 (1)
(1)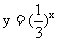


(2)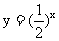


(3)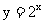


(4)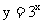


(5)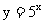


2、 过程与方法 

(1)让学生掌握指数函数的图像和性质,进一步体会指数函数的性质与底数的关系.

(2)通过特殊到一般的研究方法研究一个陌生问题是一种常规的思维方式,是由表及里的上升循环过程,学习指数函数的性质是为了更好的研究具体函数.

1、知识与技能

(1)进行复习指数函数的图像和性质,并用来解答.

(2)能够画出指数函数的图像,总结出指数函数的性质,并通过图像和性质比较指数的大小和解简单的指数不等式.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com