
1、 三位科学家因“对核糖体的结构和功能的研究”而获得2009年的诺贝尔化学奖。核糖体研究的成果之一是:通过构筑核糖体的三维模型显示不同的抗生素如何抑制细菌核糖体的功能,这些模型已被用于研发新的抗生素,拯救生命。右图为核糖体作用的机制(AA代表氨基酸),下列有关核糖体和细菌的叙述中,不正确的是
A.核糖体的功能是合成相应的蛋白质
B. 1个①上可有多个反密码子
C.细菌内只有核糖体这种细胞器
D. 组成②的基本单位有4种
20.(本小题满分14分)
已知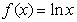 ,
,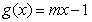 .
.
(1)若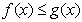 恒成立,求
恒成立,求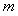 的取值范围;
的取值范围;
(2)若广东省2010届高三六校第二次联考
19.(本小题满分14分)
已知函数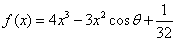 ,其中
,其中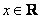 ,
,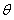 为参数,且
为参数,且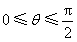 .
.
(1)当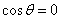 时,判断函数
时,判断函数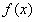 是否有极值;
是否有极值;
(2)要使函数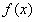 的极小值大于零,求参数
的极小值大于零,求参数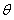 的取值范围;
的取值范围;
(3)若对(2)中所求的取值范围内的任意参数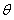 ,函数
,函数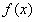 在区间
在区间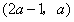 内都是增函数,求实数
内都是增函数,求实数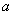 的取值范围.
的取值范围.
18.(本小题满分14分)
已知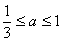 ,若
,若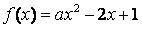 在区间
在区间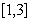 上的最大值为
上的最大值为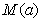 ,最小值为
,最小值为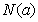 ,令
,令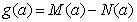 .
.
(1)求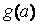 的函数表达式;
的函数表达式;
(2)判断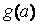 的单调性,并求出
的单调性,并求出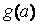 的最小值.
的最小值.
17.(本小题满分14分)
某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交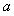 元(
元(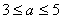 )的管理费,预计当每件产品的售价为
)的管理费,预计当每件产品的售价为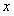 元(
元(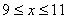 )时,一年的销售量为
)时,一年的销售量为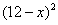 万件.
万件.
(1)求分公司一年的利润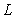 (万元)与每件产品的售价
(万元)与每件产品的售价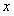 的函数关系式;
的函数关系式;
(2)当每件产品的售价为多少元时,分公司一年的利润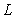 最大,并求出
最大,并求出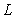 的最大值
的最大值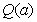 .
.
16.(本小题满分12分)
数列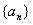 的前
的前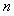 项和为
项和为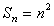 ,数列
,数列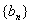 满足
满足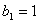 ,且
,且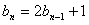 ,
,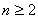 .
.
(1)求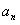 ,
,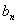 的表达式;
的表达式;
(2)设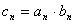 ,求数列
,求数列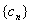 的前
的前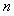 项和
项和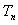 .
.
15.(本小题满分12分)
已知向量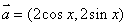 ,
,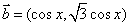 ,函数
,函数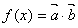 .
.
(1)求函数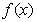 的最小正周期和值域;
的最小正周期和值域;
(2)在
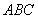 中,
中,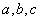 分别是角
分别是角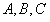 的对边,且
的对边,且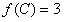 ,
,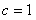 ,
,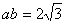 ,且
,且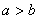 ,求
,求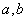 的值.
的值.
14.若定义在区间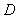 上的函数
上的函数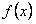 对
对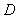 上的任意
上的任意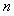 个值
个值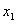 ,
,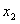 ,…,
,…,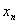 ,总满足
,总满足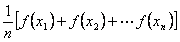 ≤
≤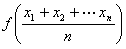 ,则称
,则称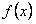 为
为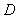 上的凸函数.已知函数
上的凸函数.已知函数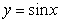 在区间
在区间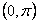 上是“凸函数”,则在△
上是“凸函数”,则在△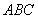 中,
中,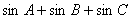 的最大值是____________.
的最大值是____________.
13.设函数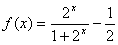 ,[
,[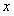 ]表示不超过
]表示不超过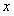 的最大整数, 则函数
的最大整数, 则函数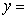 [
[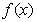 ]的值域是____________.
]的值域是____________.
12.设曲线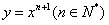 在点(1,1)处的切线与
在点(1,1)处的切线与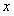 轴的交点的横坐标为
轴的交点的横坐标为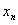 ,令
,令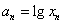 ,则
,则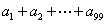 的值为____________.
的值为____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com