
⒗⑴根据余弦定理和倍角公式,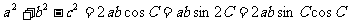 ……3分,所以
……3分,所以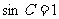 或
或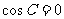 ……5分,
……5分,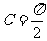 ……6分.
……6分.
⑵由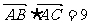 得
得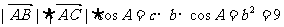 ……8分,
……8分,
即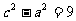 ……9分,解
……9分,解 ……10分,得
……10分,得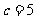 ……12分.
……12分.
⒘⑴依题意,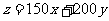 ……1分,其中
……1分,其中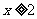 、
、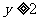 ,
,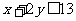 ……2分,即
……2分,即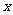 、
、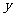 所满足的约束条件为
所满足的约束条件为 ……3分,它的所有可行解为
……3分,它的所有可行解为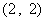 、
、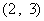 、
、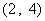 、
、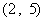 、
、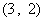 、
、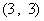 、
、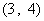 、
、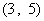 、
、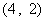 、
、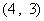 、
、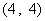 、
、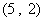 、
、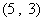 、
、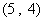 、
、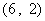 、
、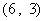 、
、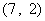 、
、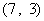 、
、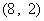 、
、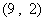 ……6分.
……6分.
⑵处理框①中的语句是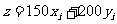 ……8分,判断框②中的语句是
……8分,判断框②中的语句是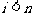 或
或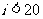
……10分,单人房人均订金为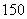 元、双人房人均订金
元、双人房人均订金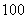 元,所以旅行团总人数最多且订单人房最多时,需要交的订金最多……11分,
元,所以旅行团总人数最多且订单人房最多时,需要交的订金最多……11分,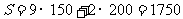 (元)……12分.
(元)……12分.
⒙⑴连接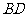 ,在
,在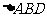 中,由余弦定理得
中,由余弦定理得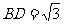 ……1分,由勾股定理逆定理得
……1分,由勾股定理逆定理得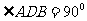 ,
,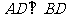 ,又因为
,又因为 ,
,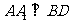 ,
,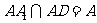 ,所以
,所以 ……2分,因为
……2分,因为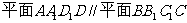 ,所以
,所以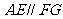 ,同理
,同理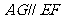 ,所以
,所以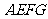 是平行四边形……3分,所以
是平行四边形……3分,所以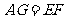 ,
,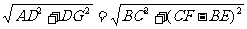 ,所以
,所以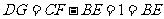 ……4分,连接
……4分,连接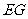 ,因为
,因为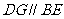 ,所以
,所以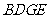 是平行四边形,
是平行四边形,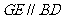 ,因为
,因为 ……5分,所以
……5分,所以 ,
,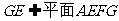 ,所以
,所以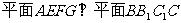 ……6分.
……6分.
⑵连接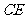 ,因为
,因为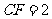 、
、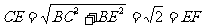 ,
,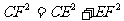 ,所以
,所以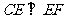 ……7分,因为
……7分,因为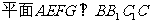 ,
,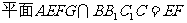 ,
, ,所以
,所以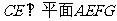 ……8分,连接
……8分,连接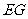 ,则
,则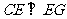 ,
,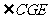 是
是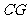 与平面
与平面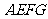 所成的角……9分,因为
所成的角……9分,因为 ,所以
,所以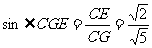 ……10分.
……10分.
⑶四边形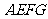 在对角面
在对角面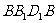 内的正投影为平行四边形,且点
内的正投影为平行四边形,且点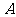 的正投影为点
的正投影为点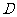
……11分,所以底面积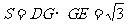 ……12分,高
……12分,高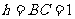 ……14分,所以棱锥的体积
……14分,所以棱锥的体积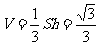 ……14分.
……14分.
方法二:⑴连接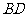 ,在
,在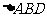 中,由余弦定理得
中,由余弦定理得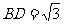 ……1分,由勾股定理逆定理得
……1分,由勾股定理逆定理得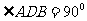 ,
,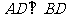 ,又因为
,又因为 ,所以以
,所以以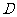 为坐标原点,
为坐标原点,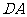 、
、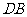 、
、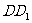 所在直线分别为
所在直线分别为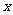 轴、
轴、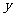 轴、
轴、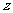 轴建立空间直角坐标系
轴建立空间直角坐标系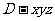 ……2分,则
……2分,则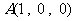 、
、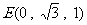 、
、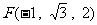 ……3分,设平面
……3分,设平面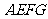 的一个法向量为
的一个法向量为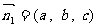 ,则
,则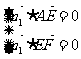 ,
,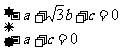 …4分,取
…4分,取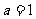 得
得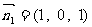 …5分,平面
…5分,平面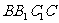 的一个法向量为
的一个法向量为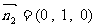 ,因为
,因为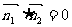 ,所以
,所以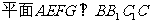 ……6分.
……6分.
⑵设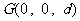 ,因为
,因为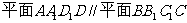 ,所以
,所以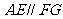 ,同理
,同理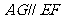 ,所以
,所以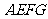 是平行四边形……7分,所以
是平行四边形……7分,所以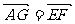 ,即
,即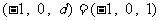 ,解得
,解得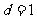 ……8分,又
……8分,又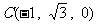 ,所以
,所以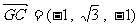 ……9分,设
……9分,设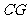 与平面
与平面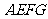 所成角为
所成角为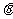 ,则
,则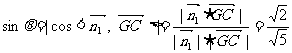 ……10分.
……10分.
⒚⑴解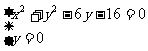 得
得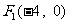 、
、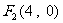 ……2分,解
……2分,解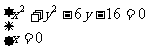 得
得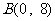 ……4分,所以
……4分,所以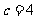 ,
, ,
,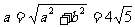 ……6分,所以椭圆
……6分,所以椭圆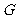 的方程是
的方程是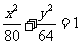 ……7分.
……7分.
⑵根据椭圆的对称性,设外切正方形一边的方程为: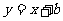 ……9分,由
……9分,由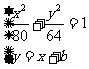 得
得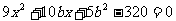 ……10分,由
……10分,由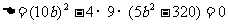 ……11分,解得
……11分,解得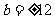 ……12分,正方形四边所在直线为
……12分,正方形四边所在直线为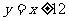 ,
,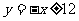 ……14分.
……14分.
⒛⑴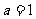 时,
时,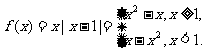 ……1分,在点
……1分,在点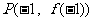 附近,
附近,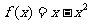 ,
,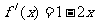 ……2分,所以
……2分,所以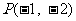 ,
,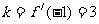 ……3分,所求切线方程为
……3分,所求切线方程为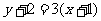 ,即
,即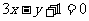 ……4分.
……4分.
⑵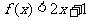 即
即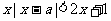 ……(*)
……(*)
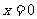 时,(*)等价于
时,(*)等价于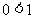 ,对任意
,对任意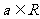 恒成立……5分.
恒成立……5分.
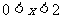 时,(*)等价于
时,(*)等价于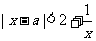 ,即
,即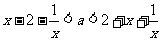 ……6分,
……6分,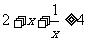 ,等号当且仅当
,等号当且仅当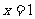 时成立…7分,
时成立…7分,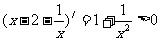 ,
,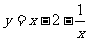 在
在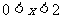 单调递增,
单调递增,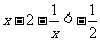 ……8分,所以
……8分,所以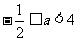 ……9分.
……9分.
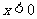 时,(*)等价于
时,(*)等价于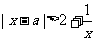 ,即
,即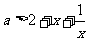 或
或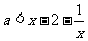 ……10分,
……10分,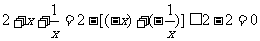 ,等号当且仅当
,等号当且仅当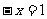 即
即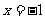 时成立……11分,所以
时成立……11分,所以 ……12分,
……12分,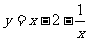 在
在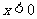 时的取值范围为
时的取值范围为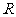 ,所以
,所以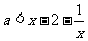 恒成立的
恒成立的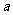 的解集为空集
的解集为空集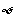 ……13分.
……13分.
所以,常数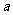 的取值范围为
的取值范围为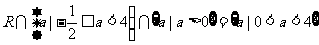 ……14分.
……14分.
21.⑴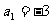 ,
,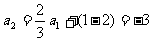 ……1分,
……1分,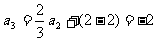 ……2分.
……2分.
⑵设 ,
,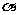 、
、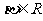 是常数……3分,代入得
是常数……3分,代入得
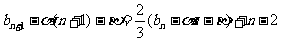 ,解
,解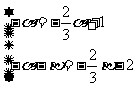 ……4分,
……4分,
得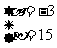 ,即
,即 ,
,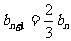 ……5分.
……5分.
若 ,则
,则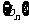 是首项为
是首项为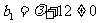 、公比为
、公比为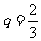 的等比数列……6分,所以
的等比数列……6分,所以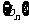 的前
的前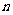 项和
项和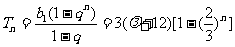 ……7分,数列
……7分,数列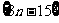 的前
的前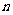 项和为
项和为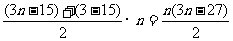 ,所以
,所以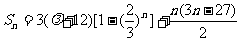 ……8分.
……8分.
若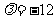 ,则
,则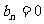 ,
,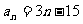 ,
,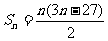 ……
……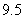 分.
分.
综上所述,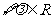 ,
,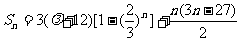 ……10分.
……10分.
⑶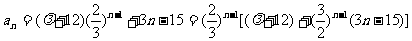 ……11分,
……11分,
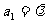 ,
,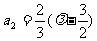 ,
,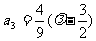 ,
,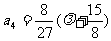 ……12分,
……12分,
当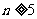 时
时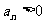 ……13分,
……13分,
所以,当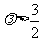 时,
时,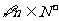 有
有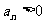 ,
,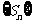 的最小项是
的最小项是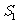 ;当
;当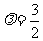 时,
时,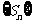 的最小项是
的最小项是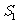 、
、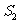 和
和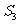 ;当
;当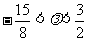 时,
时,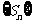 的最小项是
的最小项是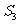 ;当
;当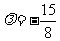 时,
时,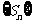 的最小项是
的最小项是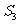 和
和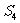 ;当
;当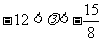 时,
时,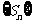 的最小项是
的最小项是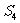 ……14分.
……14分.
⒗(本小题满分12分)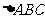 中,角
中,角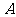 、
、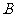 、
、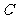 所对的边长分别为
所对的边长分别为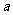 、
、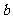 、
、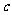 ,已知
,已知
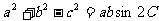 .
.
⑴求角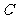 ;
;
⑵若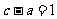 ,
,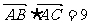 ,求
,求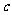 .
.
⒘(本小题满分12分)旅行社为某旅行团预订单人房和双人房两种住房,每间单人房订金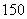 元、每间双人房订金
元、每间双人房订金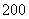 元,每种房至少预订两间(含两间),旅行团不超过13人.
元,每种房至少预订两间(含两间),旅行团不超过13人.
⑴设旅行社为这个旅行团预订了单人房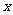 间、双人房
间、双人房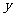 间,一共需要交订金
间,一共需要交订金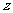 元.写出
元.写出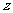 的解析式和
的解析式和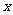 、
、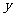 所满足的约束条件,并求它的所有可行解
所满足的约束条件,并求它的所有可行解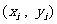 ,
,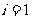 、
、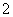 、……
、……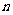 ;
;
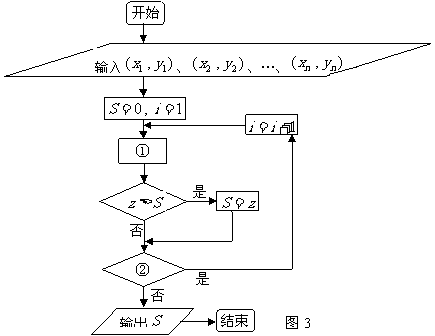 ⑵图3是根据⑴计算这个旅行团最多需交订金
⑵图3是根据⑴计算这个旅行团最多需交订金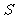 (单位:元)的程序框图.则处理框①和判断框②中的语句分别是什么?输出的
(单位:元)的程序框图.则处理框①和判断框②中的语句分别是什么?输出的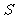 是多少?
是多少?
 ⒙(本小题满分14分)如图4,四棱柱
⒙(本小题满分14分)如图4,四棱柱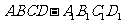 的底面
的底面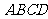 是平行四边形,
是平行四边形, ,
,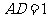 ,
,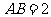 ,
,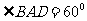 ,
,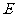 、
、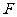 分别是侧棱
分别是侧棱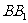 、
、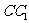 上一点,
上一点,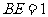 ,
,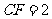 ,平面
,平面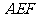 与侧棱
与侧棱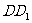 相交于
相交于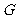 .
.
⑴证明: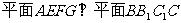 ;
;
⑵求线段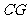 与平面
与平面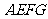 所成角的正弦值;
所成角的正弦值;
⑶求以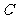 为顶点,四边形
为顶点,四边形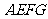 在对角面
在对角面
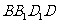 内的正投影为底面边界的棱锥的体积.
内的正投影为底面边界的棱锥的体积.
⒚(本小题满分14分)已知圆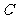 :
: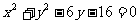 与
与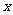 轴相交于
轴相交于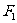 、
、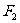 ,与
,与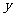 轴正半轴相交于
轴正半轴相交于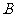 ,以
,以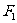 、
、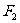 为焦点,且经过点
为焦点,且经过点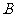 的椭圆记为
的椭圆记为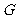 .
.
⑴求椭圆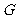 的方程;
的方程;
⑵根据椭圆的对称性,任意椭圆都有一个四边都与椭圆相切的正方形,这个正方形称为椭圆的外切正方形,试求椭圆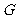 外切正方形四边所在直线的方程.
外切正方形四边所在直线的方程.
⒛(本小题满分14分)已知函数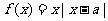 ,
,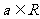 是常数.
是常数.
⑴若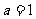 ,求
,求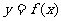 在点
在点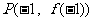 处的切线;
处的切线;
⑵是否存在常数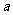 ,使
,使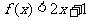 对任意
对任意 恒成立?若存在,求常数
恒成立?若存在,求常数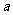 的取值范围;若不存在,简要说明理由.
的取值范围;若不存在,简要说明理由.
21.(本小题满分14分)已知数列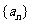 满足:
满足: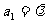 ,
,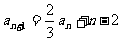 ,其中
,其中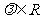 是常数,
是常数,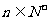 .
.
⑴若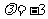 ,求
,求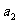 、
、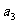 ;
;
⑵对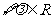 ,求数列
,求数列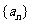 的前
的前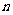 项和
项和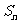 ;
;
⑶若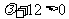 ,讨论
,讨论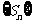 的最小项.
的最小项.
理科数学评分参考
㈠必做题(9-13题)
⒐某高中高一、高二、高三在校学生人数分别为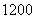 、
、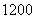 、
、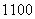 ,现要从中抽取
,现要从中抽取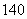 名学生参加周末公益活动,若用分层抽样的方法,则高三年级应抽取
人.
名学生参加周末公益活动,若用分层抽样的方法,则高三年级应抽取
人.
⒑下列命题中,真命题是 (将真命题前面的编号填写在横线上).
①已知平面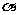 、
、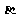 和直线
和直线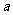 、
、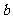 ,若
,若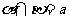 ,
, 且
且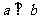 ,则
,则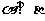 .
.
②已知平面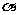 、
、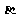 和两异面直线
和两异面直线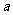 、
、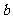 ,若
,若 ,
,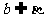 且
且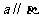 ,
,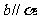 ,则
,则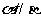 .
.
③已知平面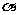 、
、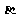 、
、 和直线
和直线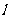 ,若
,若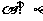 ,
,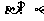 且
且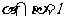 ,则
,则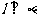 .
.
④已知平面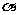 、
、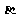 和直线
和直线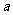 ,若
,若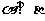 且
且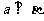 ,则
,则 或
或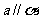 .
.
⒒由直线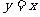 与曲线
与曲线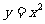 所围图形的面积
所围图形的面积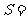 .
.
⒓函数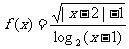 的定义域为
.
的定义域为
.
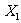
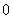
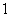
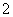
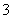
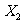
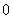
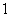
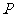
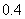
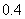
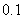
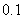
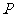
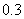
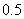
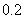
⒔产量相同的机床Ⅰ、Ⅱ生产同一种零件,它们在一小时内生产出的次品数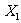 、
、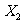 的分布列分别如下:
的分布列分别如下:
两台机床中,较好的是 ,这台机床较好的理由是 .
㈡选做题(14-15题,考生只能从中选做两题)
 ⒕(坐标系与参数方程选做题)在平面直角坐标系
⒕(坐标系与参数方程选做题)在平面直角坐标系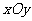 中,已知曲线
中,已知曲线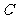 的参数方程是
的参数方程是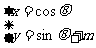 (
(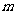 是常数,
是常数, 是参数),若曲线
是参数),若曲线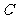 与
与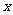 轴相切,则
轴相切,则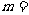 .
.
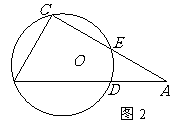
⒖(几何证明选讲选选做题)如图2,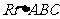 中,
中,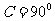 ,
,
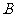
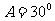 ,圆
,圆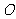 经过
经过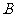 、
、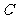 且与
且与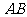 、
、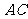 相交于
相交于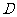 、
、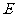 .
.
若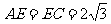 ,则
,则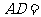 ,圆
,圆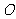 的半径
的半径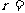 .
.
⒈已知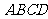 是复平面内一个平行四边形,
是复平面内一个平行四边形,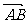 对应的复数为
对应的复数为 ,
,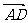 对应的复数为
对应的复数为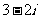 ,其中
,其中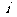 为虚数单位.则
为虚数单位.则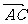 对应的复数为
对应的复数为
A. B.
B. C.
C.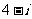 D.
D.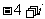
⒉已知集合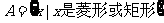 ,
,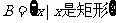 ,则
,则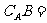
A. B.
B.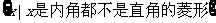
C.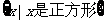 D.
D.
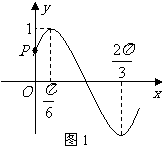 ⒊已知
⒊已知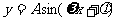 的最大值为
的最大值为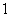 ,在区间
,在区间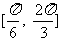 上,
上,
函数值从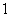 减小到
减小到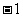 ,函数图象(如图1)与
,函数图象(如图1)与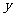 轴的交点
轴的交点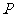
坐标是
A.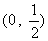 B.
B.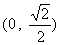 C.
C.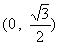 D.以上都不是
D.以上都不是
⒋经过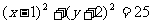 的圆心,且与向量
的圆心,且与向量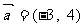 垂直的直线的方程是
垂直的直线的方程是
A.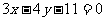 B.
B.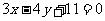 C.
C.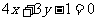 D.
D.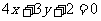
⒌已知 ,
, ,
,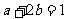 ,则
,则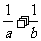 的取值范围是
的取值范围是
A. B.
B. C.
C. D.
D.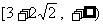
⒍从一个三棱柱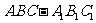 的六个顶点中任取四点,这四点不共面的概率是
的六个顶点中任取四点,这四点不共面的概率是
A.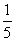 B.
B.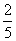 C.
C.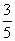 D.
D.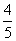
⒎若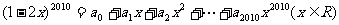 ,则
,则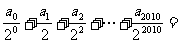
A.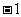 B.
B.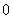 C.
C.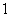 D.
D.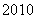
⒏用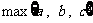 表示
表示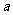 、
、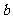 、
、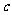 三个数中的最大值,则
三个数中的最大值,则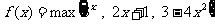 在区间
在区间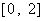 上的最大值
上的最大值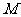 和最小值
和最小值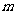 分别是
分别是
A.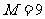 ,
,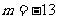 B.
B.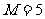 ,
,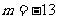
C.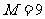 ,
,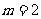 D.
D.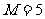 ,
,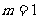
24.(20分)
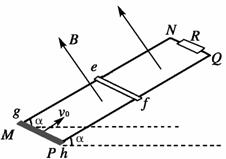
如图所示,两根平行金属导轨MN、PQ相距为d=1.0m,导轨平面与水平面夹角为α=30°,
导轨上端跨接一定值电阻R=1.6Ω,导轨电阻不计,整个装置处于与导轨平面垂直且向上的
匀强磁场中,磁感应强度大小为B=1.0T。一根与导轨等宽的金属棒ef垂直于MN、PQ静止
放置,且与导轨保持良好接触。金属棒质量m=0.1kg、电阻r=0.4Ω,距导轨底端S1=3.75m。
另一根与金属棒ef平行放置的绝缘棒gh长度也为d,质量为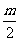 ,从导轨最低点以速度v0=10m/s沿轨道上滑并与金属棒发生正碰(碰撞时间极短),碰后金属棒沿导轨上滑S2=0.2m后再次静止,此过程中电阻R上产生的电热为Q=0.2J。已知
,从导轨最低点以速度v0=10m/s沿轨道上滑并与金属棒发生正碰(碰撞时间极短),碰后金属棒沿导轨上滑S2=0.2m后再次静止,此过程中电阻R上产生的电热为Q=0.2J。已知
两棒与导轨间的动摩擦因数均为μ=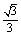 ,g取10m/s2,求:
,g取10m/s2,求:
(1)绝缘棒gh与金属棒ef碰前瞬间绝缘棒的速率;
(2)两棒碰后,安培力对金属棒做的功以及碰后瞬间金属棒的加速度;
 (3)金属棒在导轨上运动的时间。
(3)金属棒在导轨上运动的时间。
23.(18分)
如图所示,在绝缘的水平面上,相隔2L的AB两点固定有两个电量均为Q的正点电荷,C、O、D是AB连线上的三个点, O为连线的中点,CO=OD=。一质量为m、电量为q的带电物块以初速度v0从C点出发沿AB连线向B运动,运动过程中物块受到大小恒定的阻力作用,但在速度为零时,阻力也为零。当物块运动到O点时,物块的动能为初动能的n倍,到达D点刚好速度为零,然后返回做往复运动,直至最后静止在O点。已知静电力恒量为k,求:
(1)AB两处的点电荷在C点产生的电场强度的大小;
(2)物块在运动中受到的阻力的大小;
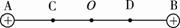 (3)带电物块在电场中运动的总路程。
(3)带电物块在电场中运动的总路程。
22.(16分)
如图所示,在高1.25m的水平桌面上,一质量为2.0kg的物块在10N的水平拉力作用下,在A处由静止开始向桌边边缘B运动, 2s末撤去水平拉力。物块运动到桌面B端后飞出落在水平地面上。已知物块与桌面之间的动摩擦因数μ=0.3,AB之间的距离为6m,不计空气阻力,g=10m/s2。求:
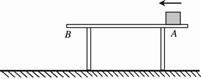 (1) 撤去水平拉力前物块加速度的大小;
(1) 撤去水平拉力前物块加速度的大小;
(2)物块离开桌面边缘B点时速度的大小;
(3)物块落地点距桌面边缘B点的水平距离。
21.(18分)
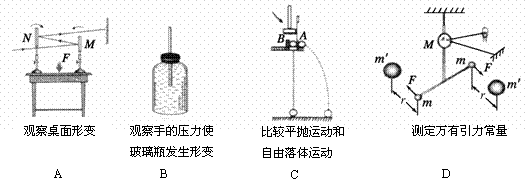
(1)在物理实验中,把一些微小量的变化进行放大,是常用的物理思想方法。如图所示的四个实验,运用此思想方法的是 。(填相应符号)
(2) 一微安电表的满偏电流为500μA,若一个100Ω的电阻与此表并联,成为一个量程为1mA的毫安表,此微安表的内阻为 Ω。若将这个毫安表改装成量程为10V的电压表,应________联一个阻值为_______Ω的电阻。
(3)“探究加速度a与物体所受合力F及质量m关系”实验。
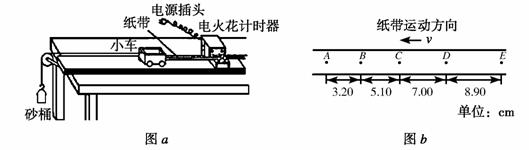
① 图a所示为实验装置图。图b为某次实验得到的一段纸带,计数点A、B、C、D、E间的时间间隔为0.1s,根据纸带可求出小车的加速度大小为 m/s2。(结果保留两位有效数字)
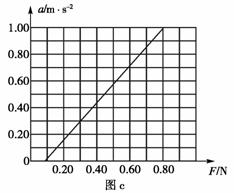 ②保持小车质量不变,改变砂和砂桶质量,进行多次测量。根据实验数据做出了加速度a随拉力F的变化图线,如图c所示。图中直线没有通过原点,其主要原因是
。
②保持小车质量不变,改变砂和砂桶质量,进行多次测量。根据实验数据做出了加速度a随拉力F的变化图线,如图c所示。图中直线没有通过原点,其主要原因是
。
③保持砂和砂桶质量不变,改变小车中砝码质量,进行多次测量,分别得到小车加速度a与质量m及对应的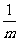 的数据如表中所示:
的数据如表中所示:
|
实验次数 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
小车加速度a/m·s -2 |
1.90 |
1.72 |
1.49 |
1.25 |
1.00 |
0.75 |
0.50 |
0.30 |
|
小车和砝码质量m/kg |
0.25 |
0.29 |
0.33 |
0.40 |
0.50 |
0.71 |
1.00 |
1.67 |
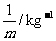 |
4.00 |
3.45 |
3.03 |
2.50 |
2.00 |
1.41 |
1.00 |
0.60 |
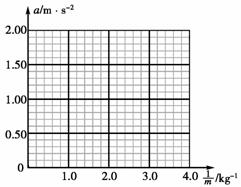 a.请在坐标纸中画出
a.请在坐标纸中画出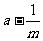 图线;
图线;
b.根据作出的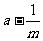 图像可以得到的结论是:
图像可以得到的结论是:
。
20.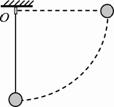 如图所示一轻质细绳一端系一质量为m的小球,绳的上端固定于O点。现用手将小球拉至水平位置(绳处于水平拉直状态),松手后小球由静止开始运动。在小球摆动过程中绳突然被拉断,绳断时与竖直方向的夹角为α。已知绳能承受的最大拉力为F,若想求出cosα值,你有可能不会求解,但是你可以通过一定的物理分析,对下列结果的合理性做出判断。根据你的判断cosα值应为
如图所示一轻质细绳一端系一质量为m的小球,绳的上端固定于O点。现用手将小球拉至水平位置(绳处于水平拉直状态),松手后小球由静止开始运动。在小球摆动过程中绳突然被拉断,绳断时与竖直方向的夹角为α。已知绳能承受的最大拉力为F,若想求出cosα值,你有可能不会求解,但是你可以通过一定的物理分析,对下列结果的合理性做出判断。根据你的判断cosα值应为
A.cosα =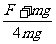 B.cosα =
B.cosα =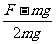
C.cosα =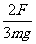 D.cosα =
D.cosα =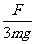
19.如图所示,在光滑的水平桌面上静止一质量为M的木块。现有A、B两颗子弹沿同一轴线,以水平速度vA、vB分别从木块两侧同时射入。子弹A、B在木块中嵌入深度分别为SA和SB。已知木块长度为L,SA 〉SB,且SA+SB〈 L,木块始终处于静止。则下列说法中正确的是
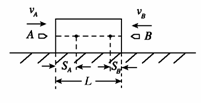 A.入射时,子弹A的速率等于子弹B的速率
A.入射时,子弹A的速率等于子弹B的速率
B.入射时,子弹A的动能大于子弹B的动能
C.在子弹运动过程中,子弹A的动量大于子弹B的动量
D.在子弹运动过程中,子弹A受到的摩擦阻力大于子弹
B受到的摩擦阻力
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com