
1.下列说法中符合物理学史实的是
A.汤姆生发现了电子,于是他提出了原子核式结构的学说
B.卢瑟福在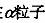 散射实验中发现放射源发出
散射实验中发现放射源发出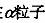 能穿透铝箔并发生散射
能穿透铝箔并发生散射
c.查德威克在原子核人工核转变的实验中发现了质子
D_爱因斯坦为解释光电效应现象提出了光子说
22.(本小题满分12分)
设函数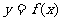 在区间D上的导函数为
在区间D上的导函数为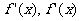 在区间D上的导函数为
在区间D上的导函数为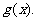 若在区间D上,
若在区间D上,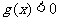 恒成立,则称函数
恒成立,则称函数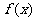 在区间D上为“凸函数”.已知实数m是常数,
在区间D上为“凸函数”.已知实数m是常数,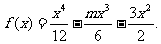
(I)若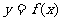 在区间[0,3]上为“凸函数”,求m的取值范围;
在区间[0,3]上为“凸函数”,求m的取值范围;
(II)若对满足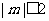 的任何一个实数m,函数
的任何一个实数m,函数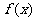 在区间(a,b)上都为“凸函数”求b-a的最大值.
在区间(a,b)上都为“凸函数”求b-a的最大值.
21.(本小题满分12分)
已知函数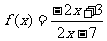 ,若存在实数
,若存在实数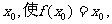 则称
则称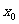 是函数
是函数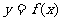 的一个不动点.
的一个不动点.
(I)求:函数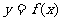 的不动点;
的不动点;
(II)已知a、b是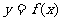 的两个不动点,且
的两个不动点,且 .当
.当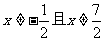 时,比较
时,比较
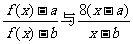 的大小;
的大小;
(III)在数列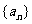 中,
中,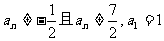 ,等式
,等式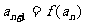 对任何正整数n都成立,求数列
对任何正整数n都成立,求数列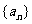 的通项公式.
的通项公式.
20.(本小题满分12分)
已知实轴长为2a,虚轴长为2b的双曲线S的焦点在x轴上,直线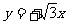 是双曲线S的一条渐近线,而且原点O,点A(a,0)和点B(0,-b)使等式
是双曲线S的一条渐近线,而且原点O,点A(a,0)和点B(0,-b)使等式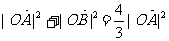 ·
·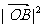 成立.
成立.
(I)求双曲线S的方程;
(II)若双曲线S上存在两个点关于直线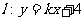 对称,求实数k的取值范围.
对称,求实数k的取值范围.
19.(本小题满分12分)
如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
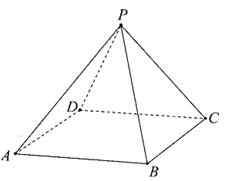 (I)求证:PD⊥BC;
(I)求证:PD⊥BC;
(II)求二面角B-PD-C的大小.
18.(本小题满分12分)
某单位组织职工参加了旨在调查职工健康状况的测试.该测试包括心理健康测试和身体健康两个项目,每个项目的测试结果为A、B、C、D、E五个等级.假设该单位50位职工全部参加了测试,测试结果如下:x表示心理健康测试结果,y表示身体健康测试结果.
 y
y |
身体健康 |
|||||
|
A |
B |
C |
D |
E |
||
|
心理健康 |
A |
1 |
3 |
1 |
0 |
1 |
|
B |
1 |
0 |
7 |
5 |
1 |
|
|
C |
2 |
1 |
0 |
9 |
3 |
|
|
D |
1 |
b |
6 |
0 |
a |
|
|
E |
0 |
0 |
1 |
1 |
3 |
(I)求a+b的值;
(II)如果在该单位随机找一位职工谈话,求找到的职工在这次测试中心理健康为D等且身体健康为C等的概率;
(III)若“职工的心理健康为D等”与“职工的身体健康为B等”是相互独立事件,求a、b的值.
17.(本小题满分10分)
已知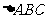 的三个内角A、B、C所对的三边分别是a、b、c,平面向量
的三个内角A、B、C所对的三边分别是a、b、c,平面向量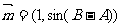 ,平面向量
,平面向量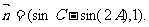
(I)如果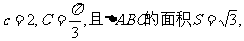 求a的值;
求a的值;
(II)若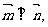 请判断
请判断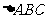 的形状.
的形状.
16.把一个半径为r的实心铁球O熔化铸成两个实心小球O1与O2,假设没有任何损耗.设铁球O的表面积为S,小球O1的半径为r1,表面积为S1,小球O2的半径为r2,两个小球的半径之比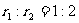 ,那么球O1的表面积与球O的表面积之比
,那么球O1的表面积与球O的表面积之比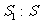 = .
= .
15.已知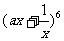 的展开式中常数项为-160,那么常数a=
.
的展开式中常数项为-160,那么常数a=
.
14.某地区共有10万户居民,该地区城市与农村住户之比为4:6,根据分层抽样方法,调查了该地区1000户居民冰箱拥有情况,调查结果如下表所示:
|
|
城市 |
农村 |
|
有冰箱 |
356(户) |
440(户) |
|
无冰箱 |
44(户) |
160(户) |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com