
1. 下列加点字的注音全都正确的一项是
A.笑靥(yè) 俨(yǎn)然 残骸(hái) 畏葸(xǐ)不前
B.聒(guā)噪 炮烙(luò) 蹂躏(lìn) 锲(qì)而不舍
C.反馈(kuì) 朱拓(tuò) 束(sù)缚 惴惴(zhuì)不安
D.徘徊(huí) 湮(yān)没 懵(méng)懂 璀(cuǐ)璨夺目
20. (本题满分16分)
已知函数f(x)=alnx+x2(a为实常数).
(1)若a=-2,求证:函数f(x)在(1,+.∞)上是增函数;
(2)求函数f(x)在[1,e]上的最小值及相应的x值;
(3)若存在x∈[1,e],使得f(x)≤(a+2)x成立,求实数a的取值范围.
第 4 页 共 4 页
江苏省海安高级中学2010届高考信息试卷
19.(本题满分16分)
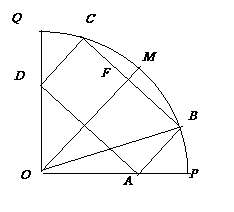
如图所示,某市政府决定在以政府大楼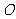 为中心,正北方向和正东方向的马路为边界的
为中心,正北方向和正东方向的马路为边界的 扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径
扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径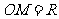 ,
,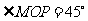 ,
,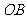 与
与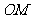 之间的夹角为
之间的夹角为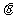 .
.
(1)将图书馆底面矩形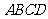 的面积
的面积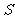 表示成
表示成 的函数.
的函数.
 (2)若
(2)若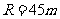 ,求当
,求当 为何值时,矩形
为何值时,矩形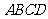 的面积
的面积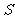 有最大值?
有最大值?
其最大值是多少?(精确到0.01m2)
17. (本题满分15分)
已知数列{an}中,a1=,点(n,2an+1-an)(n∈N*)在直线y=x上,
(Ⅰ)计算a2,a3,a4的值;
(Ⅱ)令bn=an+1-an-1,求证:数列{bn}是等比数列;
(Ⅲ)设Sn、Tn分别为数列{an}、{bn}的前n项和,是否存在实数λ,使得数列{}为等差数列?若存在,试求出λ的值;若不存在,请说明理由.
第 3 页 共 4 页
18(本题满分15分)
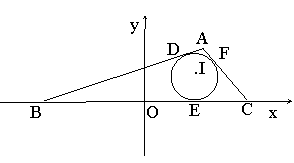
如图,△ABC的内切圆与三边AB、BC、CA的切点分别为D、E、F,已知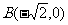 ,
C
,
C 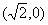 ,内切圆圆心
,内切圆圆心 .设A点的轨迹为L
.设A点的轨迹为L
(1)求L的方程;
 (2)过点C作直线
(2)过点C作直线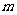 交曲线L于不同的两点M、N,问在
交曲线L于不同的两点M、N,问在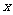 轴上是否存在一个异于点C的定点Q.使
轴上是否存在一个异于点C的定点Q.使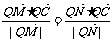 对任意的直线
对任意的直线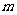 都成立?
若存在,求出Q的坐标,若不存在,说明理由.
都成立?
若存在,求出Q的坐标,若不存在,说明理由.
16. (本题满分14分)
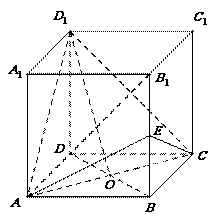 正方体
正方体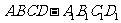 的棱长为
的棱长为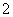 ,
,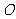 是
是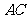 与
与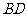 的交点,
的交点,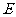 为
为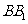 的中点.
的中点.
(Ⅰ)求证:直线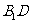 ∥平面
∥平面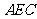 ;
;
(Ⅱ)求证: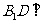 平面
平面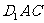 ;
;
(Ⅲ)求三棱锥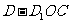 的体积.
的体积.
15、(本题满分14分)
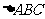 中内角
中内角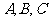 的对边分别为
的对边分别为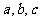 ,
,
向量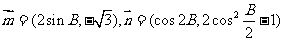 且
且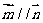
(Ⅰ)求锐角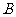 的大小,
的大小,
(Ⅱ)如果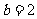 ,求
,求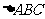 的面积
的面积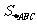 的最大值
的最大值
14、设面积为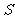 的平面四边形的第
的平面四边形的第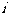 条边的边长记为
条边的边长记为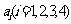 ,
,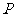 是该四边形内任意一点,
是该四边形内任意一点, 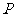 点到第
点到第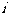 条边的距离记为
条边的距离记为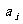 ,若
,若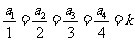 ,则
,则 .类比上述结论,体积为
.类比上述结论,体积为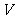 的三棱锥的第
的三棱锥的第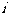 个面的面积记为
个面的面积记为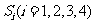 ,
,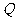 是该三棱锥内的任意一点,
是该三棱锥内的任意一点,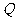 点到第
点到第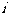 个面的距离记为
个面的距离记为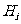 ,相应的正确命题是 ▲
w.
,相应的正确命题是 ▲
w.

第 2 页 共 4 页
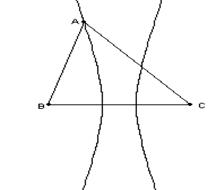
13、如右图所示的曲线是以锐角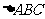 的顶点B、C为焦点,
的顶点B、C为焦点,
且经过点A的双曲线,若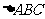 的内角的对边分别为
的内角的对边分别为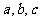 ,
,
且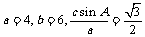 ,则此双曲线的离心率为 ▲ .
,则此双曲线的离心率为 ▲ .
12、已知两个不同的平面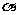 、
、 和两条不重合的直线,m、n,有下列四个命题:
和两条不重合的直线,m、n,有下列四个命题:
①若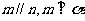 ,则
,则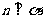
 ②若
②若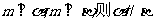 ;
;
③若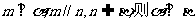 ;
;
④若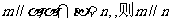
其中不正确的命题的个数是 ▲ .
11、如图所示,在一个边长为1的正方形AOBC内,曲线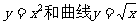 围成一个叶形图(阴影部分),向正方形AOBC内随机投一点(该点落在正方形AOBC内任何一点是等可能的),则所投的点落在叶形图内部的概率是 ▲ 种。
围成一个叶形图(阴影部分),向正方形AOBC内随机投一点(该点落在正方形AOBC内任何一点是等可能的),则所投的点落在叶形图内部的概率是 ▲ 种。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com