
18.(本小题满分12分)
甲袋和乙袋中都装有大小相同的红球和白球,已知甲袋中共有m个球,乙袋中共有2m个球,从甲袋中摸出一个球为红球的概率为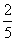 ,从乙袋中摸出一个球为红球的概率为
,从乙袋中摸出一个球为红球的概率为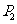 .
.
(I) 若m=10,求甲袋中红球的个数;
(II)
若将甲、乙两袋中的球装在一起后,从中摸出一个红球的概率是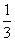 ,求出
,求出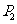 的值;
的值;
(III)
设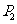 =
=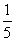 ,若从甲、乙两袋中各自有放回的摸球,每次摸出一个球,并且从甲袋中摸一次,从乙袋中摸2次.设ξ表示摸出红球的总次数,求ξ的分布列和期望.
,若从甲、乙两袋中各自有放回的摸球,每次摸出一个球,并且从甲袋中摸一次,从乙袋中摸2次.设ξ表示摸出红球的总次数,求ξ的分布列和期望.
解:(I)设甲袋中红球的个数为x,依题意得 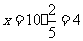 .
.
(II)由已知得: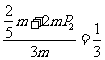 ,解得
,解得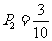 .
.
(III)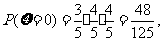
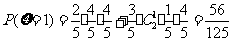
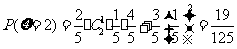
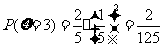
|
_ξ |
0 |
1 |
2 |
3 |
|
p |
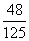 |
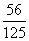 |
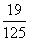 |
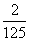 |
所以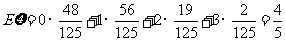
17.(本小题满分10分)
在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2a-c)cosB=bcosC.
(Ⅰ)求角B的大小;
|
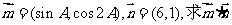 的最大值。
的最大值。
(I)∵(2a-c)cosB=bcosC,∴(2sinA-sinC)cosB=sinBcosC
即2sinAcosB=sinBcosC+sinCcosB=sin(B+C)
∵A+B+C=π,∴2sinAcosB=sinA.∵0<A<π,∴sinA≠0.
∴cosB=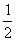 .
.
∵0<B<π,∴B=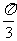 .
.
(II)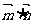 =6sinA+cos2A.=-2sin2A+6sinA+1,A∈(0,
=6sinA+cos2A.=-2sin2A+6sinA+1,A∈(0,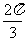 )设sinA=t,则t∈
)设sinA=t,则t∈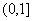 .
.
则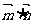 =-2t2+6t+1=-2(t-
=-2t2+6t+1=-2(t-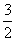 )2+
)2+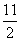 ,t∈
,t∈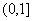 .∴t=1时,
.∴t=1时,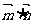 取最大值.5
取最大值.5
16.已知方程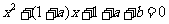 的两个实根
的两个实根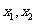 ,满足0﹤
,满足0﹤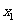 ﹤1﹤
﹤1﹤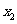 ,则
,则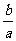 的取值范围是_
的取值范围是_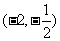 .
.
15.已知双曲线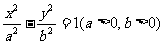 的右顶点到其渐近线的距离不大于
的右顶点到其渐近线的距离不大于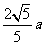 ,其离心率e的取值范围为
,其离心率e的取值范围为 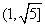 .
.
14.△ABC的三边长为1,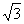 ,2,P 为平面ABC外一点,它到三顶点的距离都等于2,则P到平面ABC的距离为___
,2,P 为平面ABC外一点,它到三顶点的距离都等于2,则P到平面ABC的距离为___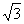 ____.
____.
13. 若二项式(x+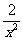 )n的展开式共7项,则展开式中的常数项为_____60__.
)n的展开式共7项,则展开式中的常数项为_____60__.
12.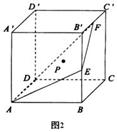 如图2,正方体AC′中,E、F分别是BB′、B′C′的中点,点P在AEF确定的平面内,且P点到A点和平面BCC′B′的距离相等,则P点轨迹是( C )
如图2,正方体AC′中,E、F分别是BB′、B′C′的中点,点P在AEF确定的平面内,且P点到A点和平面BCC′B′的距离相等,则P点轨迹是( C )
A.直线 B.抛物线 C.椭圆 D.双曲线
10.函数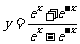 的图像大
的图像大 致为
( A ).
致为
( A ).

11直线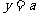 与函数
与函数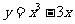 的图象有相异三个交点,则
的图象有相异三个交点,则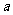 的取值范围是(
A )
的取值范围是(
A )
A.(-2,2) B.(-2,0) C.(0,2) D.(2, )
)
9.在数列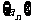 中,
中, ,则
,则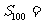 (B )
(B )
A.2100 B.2600 C.2800 D. 3100
8.已知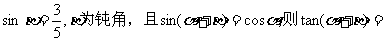 ( C )
( C )
A.1 B.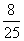 C.-2 D.2
C.-2 D.2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com