17．(本题满分15分)

已知向量= (cos ，sin )，= (cos ，−sin )， = (，−1) ，其中x∈R．

　 (I)当⊥时，求x值的集合；

(Ⅱ)求| − |的最大值．

16．(本题满分14分)

某单位用2160万元购得一块空地，计划在该地块上建造一栋至少10层，每层2000平方米的楼房。经测算，如果将楼房建为x(x ≥ 10)层，则每平方米的平均建筑费用为560 + 48x(单位：元)．

⑴写出楼房平均综合费用y关于建造层数x的函数关系式；

⑵该楼房应建造多少层时，可使楼房每平方米的平均综合费用最少？最少值是多少？

(注：平均综合费用 = 平均建筑费用 + 平均购地费用，平均购地费用 = )

15．(本题满分14分)

已知函数f (x) = 的定义域集合是A，函数 g(x) = lg [x² − (2a + 1)x + a² + a]的定义域集合是B．

(1)求集合A，B．

(2)若A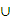B = B，求实数a的取值范围．

14．已知函数f (x) 的定义域为[−2，+∞)，部分对应值如下左表，f ' (x) 为f (x) 的导函数，函数y = f ' (x)的图象如下右图所示，若两正数a，b满足f (2a + b) < 1，则 的取值范围是　 ▲ 　．

13．下图是一组函数图像，它们分别与其后所列的一个现实情境相匹配：

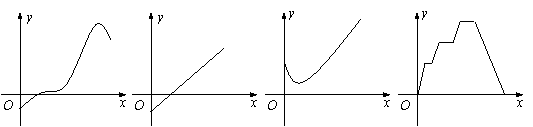
①　　　 　　　　　　②　　　　　 　　　　③　　　　　　　 　　④

情境A：一份30分钟前从冰箱里取出来，然后被放到微波炉里加热，最后放到餐桌上的食物的温度(将0时刻确定为食物从冰箱里被取出来的那一刻)；

情境B：一个1970年生产的留声机从它刚开始的售价到现在的价值(它被一个爱好者收藏，并且被保存得很好)；

情境C：从你刚开始放水洗澡，到你洗完后把水排掉这段时间浴缸里水的高度；

情境D：根据乘客人数，每辆公交车一趟营运的利润．

其中情境A，B，C，D分别对应的图象是　 ▲ 　．

12．已知集合P ={ x | x = 2ⁿ，n∈N}，Q ={ x | x = 2n，n∈N}，将集合P∪Q中的所有元素从小到大依次排列，构成一个数列{a_n}，则数列{a_n}的前20项之和S₂₀ =　 ▲ 　．

11．已知关于x的不等式 < 2的解集为P，若1ÏP，则实数a的取值范围为　 ▲ 　．

10．已知函数f (x) = sin ²ωx + sin ωx cos ωx，x∈R，又f (α) = − ，f (β) = ，若|α − β|的最小值为 ，则正数ω的值为　 ▲ 　．

9．已知对于任意实数x，函数f (x)满足f ² (−x) = f ² (x)，若方程f (x) = 0有2009个实数解，则这2009个实数解之和为　 ▲ 　．

8．已知函数y = f (x)，x∈[0，2π]的导函数y = f ' (x)的图象，

如图所示，则y = f (x) 的单调增区间为　 ▲ 　．