
16. 已知向量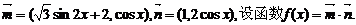
(I)求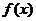 的最小正周期与单调递减区间。
的最小正周期与单调递减区间。
(II)在△ABC中,a、b、c、分别是角A、B、C的对边,若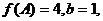 △ABC的面积为
△ABC的面积为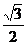 ,求
,求 的值。
的值。
15.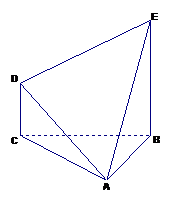 在几何体ABCDE中,
在几何体ABCDE中,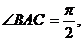 DC⊥平面ABC,EB⊥平面ABC,AB=AC=BE=2,CD=1,
DC⊥平面ABC,EB⊥平面ABC,AB=AC=BE=2,CD=1,
(I)求证:;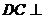 平面ABE;
平面ABE;
(II)设平面ABE与平面ACD的交线为直线l,求证: 平面BCDE;
平面BCDE;
(III)设F是BC的中点,求证:平面AFD⊥平面AFE。
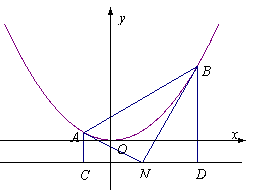
23.[必做题]如图,已知抛物线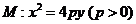 的准线为
的准线为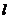 ,
,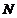 为
为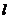 上的一个动点,过点
上的一个动点,过点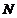 作抛物线
作抛物线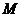 的两条切线,切点分别为
的两条切线,切点分别为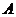 ,
,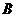 ,再分别过
,再分别过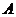 ,
,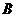 两点作
两点作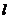 的垂线,垂足分别为
的垂线,垂足分别为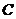 ,
,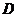 .
.
(1)求证:直线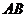 必经过
必经过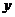 轴上的一个定点
轴上的一个定点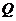 ,并写出点
,并写出点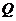 的坐标;
的坐标;
(2)若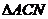 ,
,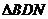 ,
, 的面积依次构成等差数列,求此时点
的面积依次构成等差数列,求此时点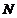 的坐标.
的坐标.
22.[必做题]某电视台综艺频道组织的闯关游戏,游戏规定前两关至少过一关才有资格闯第三关,闯关者闯第一关成功得3分,闯第二关成功得3分,闯第三关成功得4分.现有一位参加游戏者单独闯第一关、第二关、第三关成功的概率分别为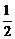 、
、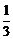 、
、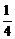 ,记该参加者闯三关所得总分为
,记该参加者闯三关所得总分为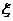 .
.
(1)求该参加者有资格闯第三关的概率;
(2)求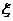 的分布列和数学期望.
的分布列和数学期望.
21.[选做题]在A,B,C,D四个小题中只能选做2个小题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
A.选修4-1:几何证明选讲
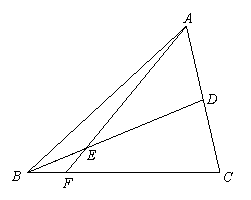 如图,在
如图,在 中,D是AC中点,E是BD三等分点,AE的延长线交BC于F,
中,D是AC中点,E是BD三等分点,AE的延长线交BC于F,
求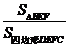 的值.
的值.
B.选修4-2:矩阵与变换
已知矩阵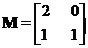 ,求矩阵
,求矩阵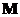 的特征值及其相应的特征向量.
的特征值及其相应的特征向量.
C.选修4-4:坐标系与参数方程
在极坐标系中,直线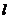 的极坐标方程为
的极坐标方程为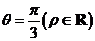 ,以极点为原点,极轴为
,以极点为原点,极轴为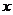 轴的正半轴建立平面直角坐标系,曲线
轴的正半轴建立平面直角坐标系,曲线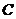 的参数方程为
的参数方程为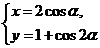 (
(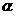 为参数),求直线
为参数),求直线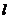 与曲线
与曲线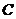 的交点P的直角坐标.
的交点P的直角坐标.
D.选修4-5:不等式选讲
已知函数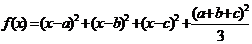 (
(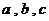 为实数)的最小值为
为实数)的最小值为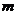 ,若
,若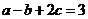 ,求
,求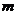 的最小值.
的最小值.
20.已知函数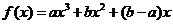 (
(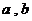 不同时为零的常数),导函数为
不同时为零的常数),导函数为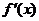 .
.
(1)当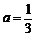 时,若存在
时,若存在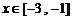 使得
使得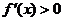 成立,求
成立,求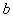 的取值范围;
的取值范围;
(2)求证:函数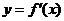 在
在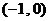 内至少有一个零点;
内至少有一个零点;
(3)若函数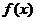 为奇函数,且在
为奇函数,且在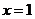 处的切线垂直于直线
处的切线垂直于直线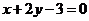 ,关于
,关于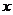 的方程
的方程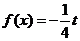 在
在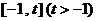 上有且只有一个实数根,求实数
上有且只有一个实数根,求实数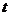 的取值范围.
的取值范围.
2010年苏北四市高三年级第二次模拟考试
数 学 (Ⅱ)
(考试时间30分钟,试卷满分40分)
19.一走廊拐角处的横截面如图所示,已知内壁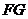 和外壁
和外壁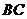 都是半径为
都是半径为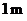 的四分之一圆弧,
的四分之一圆弧,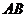 ,
,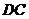 分别与圆弧
分别与圆弧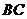 相切于
相切于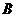 ,
,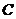 两点,
两点,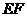 ∥
∥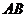 ,
,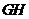 ∥
∥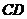 ,且两组平行墙壁间的走廊宽度都是
,且两组平行墙壁间的走廊宽度都是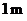 .
.
(1)若水平放置的木棒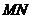 的两个端点
的两个端点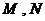 分别在外壁
分别在外壁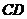 和
和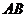 上,且木棒与内壁圆弧相切于点
上,且木棒与内壁圆弧相切于点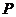 .设
.设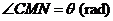 ,试用
,试用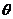 表示木棒
表示木棒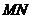 的长度
的长度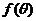 ;
;
 (2)若一根水平放置的木棒能通过该走廊拐角处,求木棒长度的最大值.
(2)若一根水平放置的木棒能通过该走廊拐角处,求木棒长度的最大值.
18.已知抛物线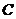 的顶点在坐标原点,准线
的顶点在坐标原点,准线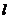 的方程为
的方程为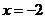 ,点
,点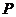 在准线
在准线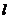 上,纵坐标为
上,纵坐标为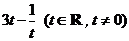 ,点
,点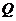 在
在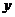 轴上,纵坐标为
轴上,纵坐标为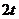 .
.
(1)求抛物线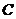 的方程;
的方程;
(2)求证:直线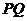 恒与一个圆心在
恒与一个圆心在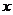 轴上的定圆
轴上的定圆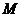 相切,并求出圆
相切,并求出圆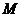 的方程。
的方程。
17. 设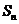 为数列
为数列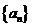 的前
的前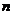 项和,若
项和,若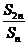 (
(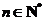 )是非零常数,则称该数列为“和等比数列”.
)是非零常数,则称该数列为“和等比数列”.
(1)若数列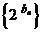 是首项为2,公比为4的等比数列,试判断数列
是首项为2,公比为4的等比数列,试判断数列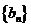 是否为“和等比数列”;
是否为“和等比数列”;
(2)若数列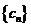 是首项为
是首项为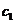 ,公差为
,公差为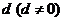 的等差数列,且数列
的等差数列,且数列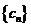 是“和等比数列”,试探究
是“和等比数列”,试探究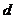 与
与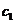 之间的等量关系.
之间的等量关系.
16.如图,在正三棱柱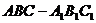 中,点
中,点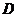 是棱
是棱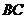 的中点.求证:
的中点.求证:
(1)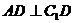 ;
;
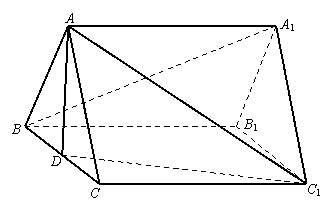 (2)
(2)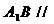 平面
平面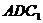 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com