
7.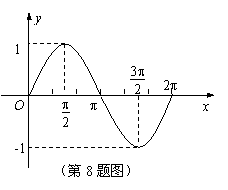 已知a,b,c是锐角△ABC中∠A,∠B,∠C的对边,若a = 3,b = 4,△ABC的面积为3,则c = ▲ .
已知a,b,c是锐角△ABC中∠A,∠B,∠C的对边,若a = 3,b = 4,△ABC的面积为3,则c = ▲ .
6.已知关于t的方程t2 −2t + a = 0的一个根为1 + i(a∈R),则实数a的值为 ▲ .
5.a,b,c成等比数列,则方程ax2 + bx + c = 0的实根有 ▲ 个.
4.已知向量 = (sin 55°,sin 35°), = (sin 25°,sin 65°),则向量 与 的夹角为 ▲ .
3.函数y = ex + e−x(e是自然对数的底数)的值域是 ▲ .
2.在△ABC 中,“B=60°”是“A,B,C 成等差数列”的 ▲ 条件(指充分性和必要性).
1.已知P = {−1,0,},Q = { y | y = sin θ,θ∈R},则P ∩ Q = ▲ .
20、(本小题满分16分)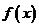 是定义在D上的函数,若对任何实数
是定义在D上的函数,若对任何实数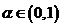 以及D中的任意两数
以及D中的任意两数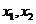 ,恒有
,恒有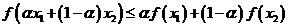 ,则称
,则称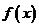 为定义在D上的C函数.
为定义在D上的C函数.
(Ⅰ)试判断函数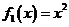 ,
,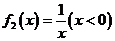 中哪些是各自定义域上的C函数,并说明理由;
中哪些是各自定义域上的C函数,并说明理由;
(Ⅱ)已知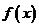 是R上的C函数,m是给定的正整数,设
是R上的C函数,m是给定的正整数,设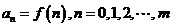 ,且
,且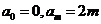 ,记
,记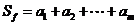 . 对于满足条件的任意函数
. 对于满足条件的任意函数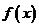 ,试求
,试求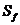 的最大值;
的最大值;
解:(Ⅰ)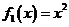 是C函数,证明如下:
是C函数,证明如下:
对任意实数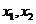 及
及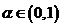 ,
,
有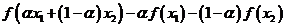
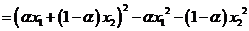
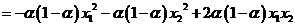
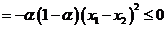 .
.
即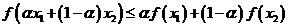 .
.
∴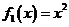 是C函数.
是C函数.
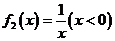 不是C函数,证明如下:
不是C函数,证明如下:
取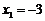 ,
,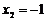 ,
,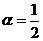 ,
,
则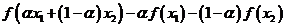
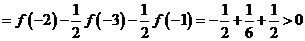 .
.
即 .
.
∴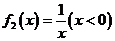 不是C函数.
不是C函数.
(Ⅱ) 对任意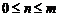 ,取
,取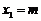 ,
,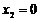 ,
,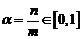 .
.
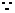
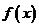 是R上的C函数,
是R上的C函数,
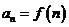 ,且
,且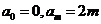
∴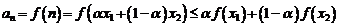
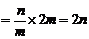 .
.
那么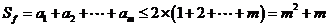 .
.
可证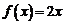 是C函数,且使得
是C函数,且使得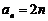
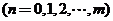 都成立,此时
都成立,此时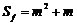 .
.
综上所述,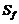 的最大值为
的最大值为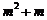 .
.

19.(本小题满分15分)
将数列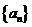 中的所有项按每一行比上一行多一项的规则排成如下数表:
中的所有项按每一行比上一行多一项的规则排成如下数表:
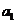
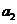
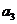
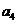
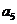
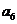
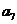

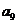
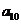
……
记表中的第一列数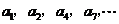 构成的数列为
构成的数列为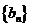 ,
,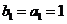 .
.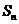 为数列
为数列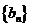 的前
的前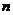 项和,且满足
项和,且满足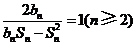 .
.
(Ⅰ)证明数列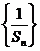 成等差数列,并求数列
成等差数列,并求数列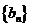 的通项公式;
的通项公式;
(Ⅱ)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当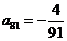 时,求上表中第
时,求上表中第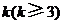 行所有项的和.
行所有项的和.
解:(Ⅰ)证明:由已知,当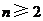 时,
时,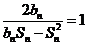 ,又
,又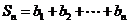 ,
,
所以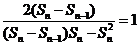
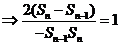
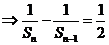 ,
,
又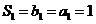 .所以数列
.所以数列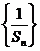 是首项为1,公差为
是首项为1,公差为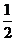 的等差数列.
的等差数列.
由上可知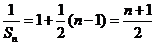 ,
,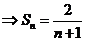 .
.
所以当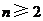 时,
时,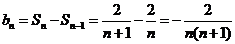 .
.
因此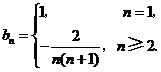
(Ⅱ)解:设上表中从第三行起,每行的公比都为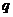 ,且
,且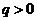 .
.
因为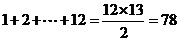 ,
,
所以表中第1行至第12行共含有数列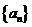 的前78项,故
的前78项,故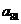 在表中第13行第三列,
在表中第13行第三列,
因此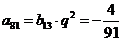 .又
.又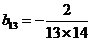 ,所以
,所以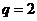 .
.
记表中第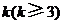 行所有项的和为
行所有项的和为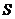 ,
,
则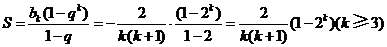 .
.
18.已知圆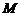 :
: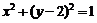 ,设点
,设点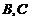 是直线
是直线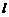 :
: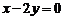 上的两点,它们的横坐标分别是
上的两点,它们的横坐标分别是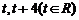 ,点
,点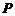 在线段
在线段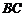 上,过
上,过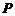 点作圆
点作圆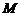 的切线
的切线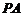 ,切点为
,切点为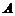 .
.
(1)若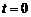 ,
,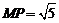 ,求直线
,求直线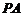 的方程;
的方程;
(2)经过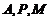 三点的圆的圆心是
三点的圆的圆心是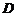 ,求线段
,求线段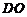 长的最小值
长的最小值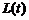 .
.
解:(1)设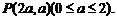

解得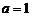 或
或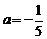 (舍去).
(舍去).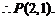
由题意知切线PA的斜率存在,设斜率为k.
所以直线PA的方程为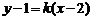 ,即
,即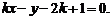
 直线PA与圆M相切,
直线PA与圆M相切,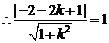 ,解得
,解得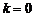 或
或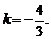
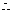 直线PA的方程是
直线PA的方程是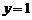 或
或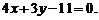
(2)设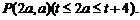
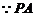 与圆M相切于点A,
与圆M相切于点A,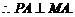
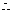 经过
经过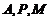 三点的圆的圆心D是线段MP的中点.
三点的圆的圆心D是线段MP的中点.
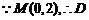 的坐标是
的坐标是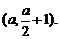
设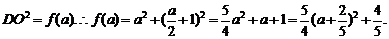
当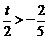 ,即
,即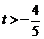 时,
时,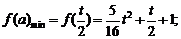
当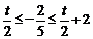 ,即
,即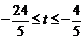 时,
时,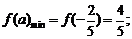
当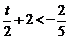 ,即
,即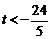 时
时
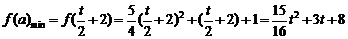
则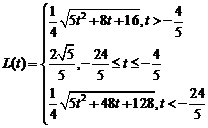
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com