
17.(本小题满分15分)如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,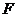 为
为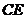 上的点,且BF⊥平面ACE.
上的点,且BF⊥平面ACE.
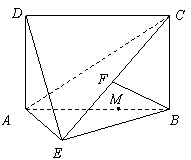 (1)求证:AE⊥BE;
(1)求证:AE⊥BE;
(2)求三棱锥D-AEC的体积;
(3)设M在线段AB上,且满足AM=2MB,试在线段
CE上确定一点N,使得MN∥平面DAE.
(1)证明: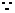
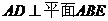 ,
,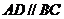
∴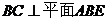 ,则
,则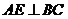 …………2分
…………2分
又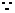
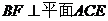 ,则
,则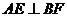
∴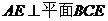 又
又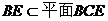 ∴
∴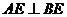 ………… 6分
………… 6分
(2)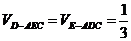 ×
×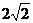 ×
×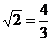 ………………………………9分
………………………………9分
(3)在三角形ABE中过M点作MG∥AE交BE于G点,在三角形BEC中过G点作GN∥BC交EC于N点,连MN,则
由比例关系易得CN=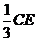 ……………………………… 11分
……………………………… 11分
 MG∥AE MG
MG∥AE MG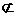 平面ADE, AE
平面ADE, AE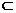 平面ADE,
平面ADE,
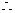 MG∥平面ADE
MG∥平面ADE
同理, GN∥平面ADE………………………………14分
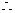 平面MGN∥平面ADE
平面MGN∥平面ADE
又MN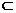 平面MGN
平面MGN  MN∥平面ADE
MN∥平面ADE
 N点为线段CE上靠近C点的一个三等分点………………16分
N点为线段CE上靠近C点的一个三等分点………………16分
16.(本小题满分14分)设函数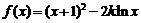 .
.
(1)当k=2时,求函数f(x)的增区间;
(2)当k<0时,求函数g(x)=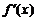 在区间(0,2]上的最小值.
在区间(0,2]上的最小值.
解(1)k=2,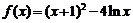 .则
.则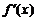 =
=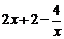 .…………………3分
.…………………3分
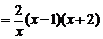 >0,(此处用“≥”同样给分) ……………………………………5分
>0,(此处用“≥”同样给分) ……………………………………5分
注意到x>0,故x>1,于是函数的增区间为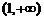 .(写为
.(写为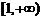 同样给分)……7分
同样给分)……7分
(2)当k<0时,g(x)=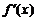 =
=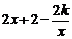 .g(x)=
.g(x)=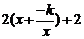 ≥
≥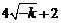 ………9分
………9分
当且仅当x=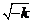 时,上述“≥”中取“=”.
时,上述“≥”中取“=”.
①若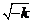 ∈
∈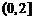 , 即当k∈
, 即当k∈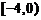 时,函数g(x)在区间
时,函数g(x)在区间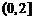 上的最小值为
上的最小值为
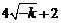 ;………………11分
;………………11分
②若k<-4,则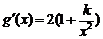 在
在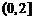 上为负恒成立,
上为负恒成立,
故g(x)在区间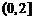 上为减函数,
上为减函数,
于是g(x)在区间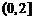 上的最小值为g(2)=6-k.
……………………………………13分
上的最小值为g(2)=6-k.
……………………………………13分
综上所述,当k∈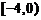 时,函数g(x)在区间
时,函数g(x)在区间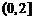 上的最小值为
上的最小值为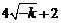 ;
;
当k<-4时,函数g(x)在区间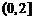 上的最小值为6-k.
………………………15分
上的最小值为6-k.
………………………15分
15.(本小题满分14分)已知角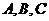 为
为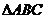 的三个内角,其对边分别为
的三个内角,其对边分别为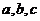 ,若
,若 ,
,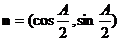 ,
,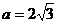 ,且
,且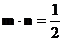 .
.
(1)求角A的值.
(2)求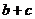 的取值范围.
的取值范围.
解:(1)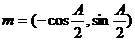 ,
,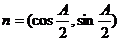 ,且
,且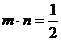 .
.
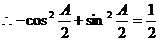 ,即
,即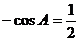 ,又
,又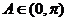 ,
,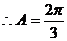 ………………………………………………….
5分
………………………………………………….
5分
(2)由正弦定理得: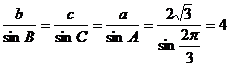 ,又
,又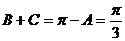 ,
,
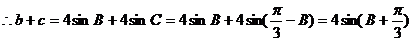 ………………8分
………………8分
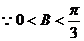 ,则
,则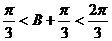 .则
.则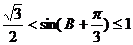 ,即
,即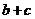 的取值范围是
的取值范围是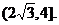 …10分
…10分
14.设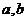 为互不相等的正整数,方程
为互不相等的正整数,方程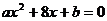 的两个实根为
的两个实根为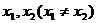 ,且
,且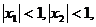 ,则
,则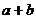 的最小值为_____▲______.9
的最小值为_____▲______.9
13.已知椭圆方程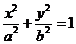
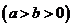 ,当
,当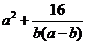 的最小值时,椭圆的离心率
的最小值时,椭圆的离心率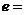 ▲ .
▲ .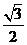
12. 设实数
设实数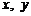 满足
满足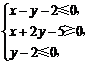 则
则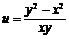 的取值范围是 ▲
.
的取值范围是 ▲
.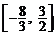
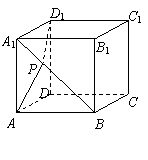
11.如右图所示,在单位正方体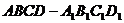 的面对角线
的面对角线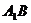 上存在一点
上存在一点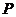 使得
使得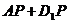 最短,则
最短,则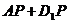 的最小值为 .
的最小值为 . 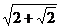
10.直线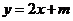 和圆
和圆 交于点A、B,以
交于点A、B,以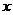 轴的正方向为始边,OA为终边(O是坐标原点)的角为
轴的正方向为始边,OA为终边(O是坐标原点)的角为 ,OB为终边的角为
,OB为终边的角为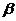 ,若
,若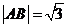 ,那么
,那么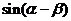 的值是
的值是
_____▲____.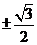
8.若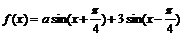 是偶函数,则
是偶函数,则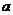 = ▲_ . a=-3,
= ▲_ . a=-3,
9.已知数列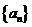 中,
中,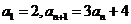 .则数列
.则数列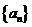 的通项公式是___
的通项公式是___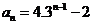 ___ .
___ .
7.设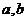 是两条不同直线,
是两条不同直线,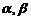 是两个不同平面,给出下列四个命题:①若
是两个不同平面,给出下列四个命题:①若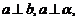
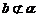 ,则
,则 ;②若
;②若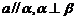 ,则
,则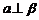 ;③若
;③若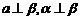 ,则
,则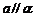 或
或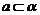 ;④若
;④若 则
则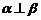 .其中正确的命题是_____▲____(请把所有正确命题的序号都填上).134
.其中正确的命题是_____▲____(请把所有正确命题的序号都填上).134
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com