
3. (深圳一模)加速度不变的运动 D
A.一定是直线运动 B.一定是曲线运动
C.可能是圆周运动 D.可能是曲线运动
2、(2010年1月广东六校联考)如图所示两个内壁光滑、半径不同的半球形碗,放在不同高度的水平面上,使两碗口处于同一水平面.现将质量相同的两个小球(小球半径远小于碗的半径),分别从两个碗的边缘由静止释放(忽略空气阻力),则:BC
 A.过最低点时两小球的速度大小相等
A.过最低点时两小球的速度大小相等
B.两小球机械能对比,始终相等
C.过最低点后两小球将滚到碗的另一侧边缘且不溜出
D.在最低点两小球对碗底的压力大小不相等,半径大的压力大
1.(2010年1月广东六校联考)9、如图所示,足够长的水平直轨道MN上左端有一点C,过MN的竖直平面上有两点A、B,A点在C点的正上方,B点与A点在一条水平线上,不计轨道阻力和空气阻力,下面判断正确的是:AD
A. 在A、C两点以相同的速度同时水平向右抛出两小球,两球一定会相遇
B. 在A、C两点以相同的速度同时水平向右抛出两小球,两球一定不会相遇
C. 在A点水平向右抛出一小球,同时在B点由静止释放一小球,两球一定会相遇
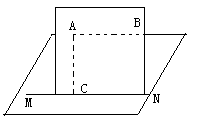 D. 在A、C两点以相同的速度同时水平向右抛出两小球,并同时在B点由静止释放一小球,三个球有可能在水平轨道上相遇
D. 在A、C两点以相同的速度同时水平向右抛出两小球,并同时在B点由静止释放一小球,三个球有可能在水平轨道上相遇
例6.已知函数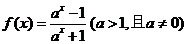 .
.
(1)求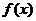 的定义域和值域;(2)讨论
的定义域和值域;(2)讨论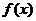 单调性.
单调性.
分析:函数的性质都要在函数的定义域范围内研究.讨论函数的单调性可以利用单调性的定义,也可以利用指数函数的范围求得判断.
解:(1)对任意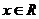 ,
,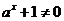 恒成立,即
恒成立,即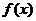 的定义域为
的定义域为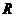 ,
,
令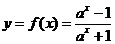 ,则
,则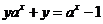 ,
,
得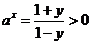 ,即
,即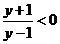 ,
,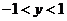 ,
,
即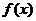 的值域为
的值域为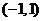 ;
;
(2)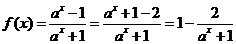 ,
,
当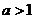 时,
时,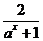 为减函数,
为减函数,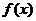 为
为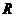 上的增函数;
上的增函数;
当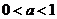 时,
时,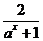 为增函数,
为增函数,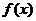 为
为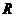 上的减函数.
上的减函数.
练习6: 已知函数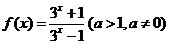 .
.
(1)求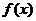 的定义域和值域;(2)讨论
的定义域和值域;(2)讨论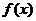 单调性.
单调性.
解:(1)要使函数有意义,需使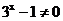 ,即
,即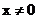 ,所以函数的定义域为
,所以函数的定义域为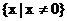
(2)函数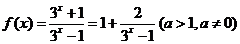
当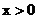 时,
时,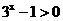 ,所以
,所以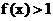 ;
;
当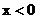 时,
时,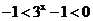 ,所以
,所以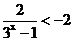 所以
所以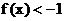 ;
;
综上函数的值域为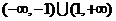 .
.
(3)设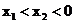 ,则
,则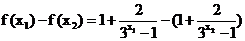
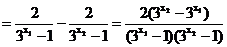 ,因为
,因为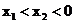 ,函数
,函数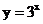 为增函数,所以
为增函数,所以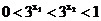 ,所以
,所以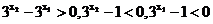 ,所以
,所以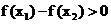 ,所以函数
,所以函数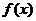 在
在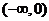 上单调递减;设
上单调递减;设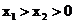 ,同理,
,同理,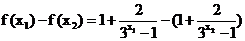
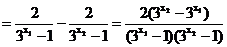 ,因为
,因为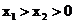 ,函数
,函数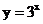 为增函数,所以
为增函数,所以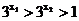 ,所以
,所以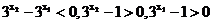 ,所以
,所以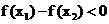 ,所以函数
,所以函数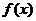 在
在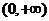 上单调递减.
上单调递减.
课堂小结:指数函数是建立在指数运算的基础上的,所以首先要掌握指数的运算,而指数函数的图象与性质又是这部分内容的重中之重,特别是指数函数的值域和单调性与奇偶性需要掌握熟练.
例5. 比较下列各组数的大小:
(1)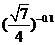 和
和
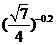 ; (2)
; (2)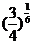 和
和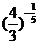 ; (3)
; (3)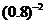 和
和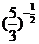 .
.
分析:可以根据指数函数的单调性比较两个指数的大小.注意化为同底,不能同底的则要根据两个数的大体范围借助中间量比较出来.
解: (1) 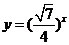 在
在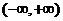 上是减函数,又
上是减函数,又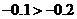 ,故
,故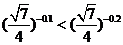 ;
;
(2)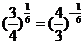 ,由
,由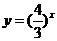 的单调性可得,
的单调性可得,
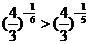 ,即
,即 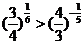 ;
;
(3)由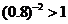 而
而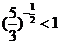 ,可知
,可知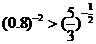 .
.
练习5. 比较下列各组数的大小:
(1)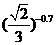 和
和
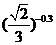 ; (2)
; (2)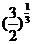 和
和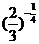 ; (3)
; (3)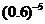 和
和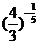 .
.
解: (1) 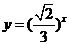 在
在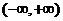 上是减函数,又
上是减函数,又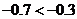 ,故
,故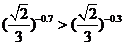 ;
;
(2)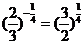 ,由
,由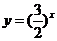 的单调性可得,
的单调性可得,
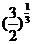
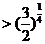 ,即
,即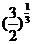
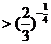 ;
;
(3)由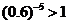 而
而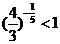 ,可知
,可知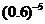 >
>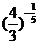 .
.
例4.(1)函数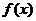 是奇函数,且当
是奇函数,且当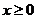 时,
时,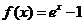 ,则
,则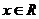 时,
时,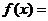 _____.
_____.
(2)设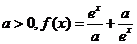 是
是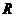 上的偶函数,则
上的偶函数,则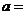 ________________.
________________.
分析:从图象上来看,奇偶函数的图象具备对称性,从奇偶性函数的定义来看,已知一段上的解析式可以求另一段的解析式.
解:(1)当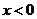 时,得
时,得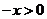 ,则
,则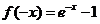 ,而函数
,而函数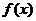 是奇函数,则
是奇函数,则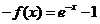 ,即
,即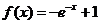 ,则
,则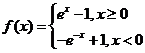 .
.
(2)因为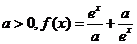 是
是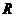 上的偶函数,所以
上的偶函数,所以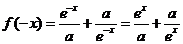 ,所以
,所以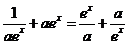 ,所以
,所以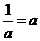 ,而
,而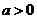 ,则
,则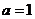 .
.
练习4.(1)定义在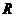 上的函数
上的函数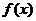 是奇函数,且当
是奇函数,且当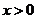 时,
时,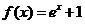 ,则
,则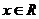 时,
时,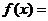 __________.
__________.
(2)已知函数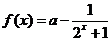 ,若
,若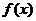 为奇函数,则
为奇函数,则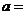 ________________.
________________.
解: (1)当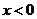 时,得
时,得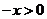 ,则
,则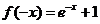 ,而函数
,而函数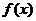 是奇函数,则
是奇函数,则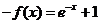 ,即
,即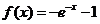 ;当
;当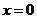 时,函数
时,函数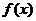 是定义在
是定义在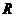 上的奇函数,得
上的奇函数,得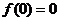 ,则
,则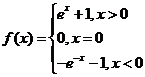 .
.
(2)因为函数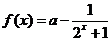 为奇函数,所以
为奇函数,所以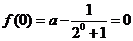 ,所以
,所以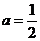 .
.
例3. 函数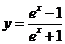 的值域
的值域
分析:此函数中只含有指数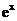 ,可以根据指数函数的取值范围,得到所求函数的值域.
,可以根据指数函数的取值范围,得到所求函数的值域.
解:由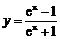 ,得
,得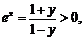 所以
所以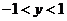 ,所以函数
,所以函数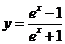 的值域为
的值域为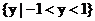 .
.
练习3:求函数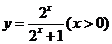 的值域.
的值域.
解:因为 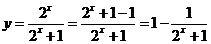 ,而
,而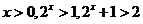 ,
,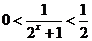 ,所以
,所以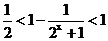 ,所以函数的值域为
,所以函数的值域为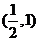 .
.
例2. 求下列函数的定义域:
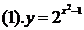
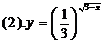

分析:指数函数要有意义,其指数可取任意实数,但出现根式,分式等还要使根式,分式有意义.
解:(1)函数有意义,则指数为任意实数,所以函数的定义域为R.
(2)函数要有意义,需使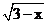 有意义,所以
有意义,所以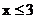 ,函数的定义域为
,函数的定义域为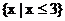

练习2.求下列函数的定义域:
(1)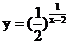 (2)
(2)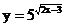
解:(1)函数要有意义,需使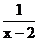 有意义,即
有意义,即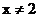 ,所以函数的定义域为
,所以函数的定义域为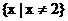 .
.
(2)函数要有意义,需使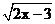 有意义,即
有意义,即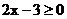 ,所以函数的定义域为
,所以函数的定义域为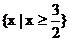 .
.
例1.化简: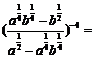 .
.
解析: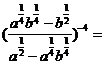
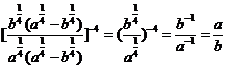 .
.
答案: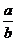

练习1:计算:(1)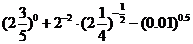

(2).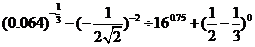 .
.
解:(1)原式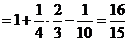

(2)原式=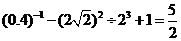 .
. 
7. 根据化合物中元素原子个数确定化学式
例7 超导材料为具有零电阻的反磁性的物质,以Y2O3、BaCO3和CuO为原料经研磨烧结可合成一种高温超导物质Y2Ba4Cu6Ox,假设在研磨烧结过程中各元素的化合价无变化,则该化合物的化学式为_________。
分析:给出的Y2O3、BaCO3和CuO中各元素的化合价分别为Y:+3、O:-2、Ba:+2、Cu:+2,在研磨烧结过程中各元素的化合价无变化,根据化合物中元素化合价的代数和为零可得出: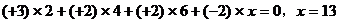 。因此该化合物的化学式为Y2Ba4Cu6O13。
。因此该化合物的化学式为Y2Ba4Cu6O13。
[点拨] 分子是由原子构成的,只要搞清了构成物质的分子中各原子的数目,书写化学式就显得轻而易举了。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com