函数的单调性一般是先根据图象判断，再利用定义证明．画函数图象通常借助计算机，求函数的单调区间时必须要注意函数的定义域，单调性的证明一般分五步：

取 值 → 作 差 → 变 形 → 定 号 → 下结论

(二)典型例题

例1．(教材P₃₄例1)根据函数图象说明函数的单调性．

解：(略)

巩固练习：课本P₃₈练习第1、2题

例2．(教材P₃₄例2)根据函数单调性定义证明函数的单调性．

解：(略)

巩固练习：

1 课本P₃₈练习第3题；

　　　 2 证明函数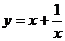在(1，+∞)上为增函数．

例3．借助计算机作出函数y =－x² +2 | x | + 3的图象并指出它的的单调区间．

解：(略)

思考：画出反比例函数的图象．

　　　 1 这个函数的定义域是什么？

　　　 2 它在定义域I上的单调性怎样？证明你的结论．

说明：本例可利用几何画板、函数图象生成软件等作出函数图象．

(一)函数单调性定义

1．增函数

　　　 一般地，设函数y=f(x)的定义域为I，

　　　 如果对于定义域I内的某个区间D内的任意两个自变量x₁，x₂，当x₁<x₂时，都有f(x₁)<f(x₂)，那么就说f(x)在区间D上是增函数(increasing function)．

思考：仿照增函数的定义说出减函数的定义．(学生活动)

注意：

1 函数的单调性是在定义域内的某个区间上的性质，是函数的局部性质；

2 必须是对于区间D内的任意两个自变量x₁，x₂；当x₁<x₂时，总有f(x₁)<f(x₂) ．

2．函数的单调性定义

如果函数y=f(x)在某个区间上是增函数或是减函数，那么就说函数y=f(x)在这一区间具有(严格的)单调性，区间D叫做y=f(x)的单调区间：

　　　 3．判断函数单调性的方法步骤

　　　　　　　 利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤：

　　　　　　　 1 任取x₁，x₂∈D，且x₁<x₂；

　　　　　　　 2 作差f(x₁)－f(x₂)；

3 变形(通常是因式分解和配方)；

4 定号(即判断差f(x₁)－f(x₂)的正负)；

5 下结论(即指出函数f(x)在给定的区间D上的单调性)．

3．f(x) = x²

　　　 1在区间 ____________ 上，f(x)的值随

着x的增大而 ________ ．

　　　 2 在区间 ____________ 上，f(x)的值随

着x的增大而 ________ ．

2．f(x) = -2x+1

　　　 1 从左至右图象上升还是下降 ______?

　　　 2 在区间 ____________ 上，随着x的增

大，f(x)的值随着 ________ ．

1．f(x) = x

　　　 1 从左至右图象上升还是下降 ______?

　　　 2 在区间 ____________ 上，随着x的增

大，f(x)的值随着 ________ ．

2．　 画出下列函数的图象，观察其变化规律：

1．　 观察下列各个函数的图象，并说说它们分别反映了相应函数的哪些变化规律：

1 随x的增大，y的值有什么变化？

2 能否看出函数的最大、最小值？

3 函数图象是否具有某种对称性？

课本P₂₈ 习题1．2(A组) 第8-12题 (B组)第2、3题

理解函数的三种表示方法，在具体的实际问题中能够选用恰当的表示法来表示函数，注意分段函数的表示方法及其图象的画法．