
(三)地貌对人类经济建设有十分重要的影响,尤其对农业生产、工程建设、城市发展和旅游的影响最为显著。
7.下列关于地貌对农业生产影响的叙述,正确的是
A.平原和盆地地形都适合发展种植业 B.较高海拔的山地适合发展水果生产
C.高海拔的高原适合发展高原畜牧业 D.坡度>25°的山地可采取等高种植
8.下列关于地貌特点成为工程建设难题的叙述,正确的是
A.高寒、冻土是制约云贵地区铁路建设的工程难题
B.地面沉降是制约喀斯特地区水利建设的工程难题
C.海水倒灌是制约平原地区施工建设的工程性难题
D.地基松软多流沙是制约上海地铁建设的工程难题
9.下列关于城市地域扩展的叙述,正确的是
A.兰州等地处河谷中的城市多线性狭长延伸
B.北京等地处平原上的城市多呈立体状扩展
C.重庆等地处山区的城市向四周放射状发展
D.上海等 沿江城市主要沿河道两岸跃动扩展
沿江城市主要沿河道两岸跃动扩展
10.下列人类改造地貌的活动,最容易产生负面影响而不利于科学发展的做法是
A.修筑梯田 B.围湖造田 C.挖掘河道 D.填海造陆
(二)地球的运动给地球环境和人类的生产生活带来一系列深刻的影响,地球运动周期已成为人类测量时间的尺度。
3.埃及友人来我国参观上海世博会。飞机在开罗时间(东二区)早晨6时起飞,在北京时间22时抵达浦东国际机场,这架飞机大约飞行了
A.10小时 B.12小时 C.14小时 D.16小时
4.上海和埃及开罗纬度位置大致相同,两地大致相同的地理现象是
①地方时 ②昼夜长短 ③季节更替 ④正午太阳高度
A.①②③ B.①②④ C.①③④ D.②③④
5.下列日期中,上海地区日出最早、正午太阳高度最大的一天是
A.4月5日 B.7月1日 C.10月1日 D.12月22日
6.埃及参加2010年上海世博览会,其展馆布置将呈现的文化特色是
A.南亚文化 B.伊斯兰文化 C.非洲文化 D.西欧文化
(一)飞向太空一直是炎黄子孙的梦想。从嫦娥奔月的神话传说到敦煌石窟的飞天壁画,华夏儿女从未停止过登上月球的向往。目前我国正在实施的“嫦娥工程”,必将实现国人的美好愿望。
1.月球表面最明显的特征是
A.月面坦荡地势很平缓 B.月岩裸露月壤很浅薄
C.山岭起伏环行山密布 D.海面广阔两极有冰层
2.新月和满月经常有,但日食与月食不常见的原因是
A.月球自转周期与月球公转周期不同 B.月球自转方向与月球公转方向不同
C.月球公转周期与月相变化周期不同 D.月球与地球两者公转轨道平面斜交
22.(本小题满分14分)
已知双曲线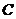 :
: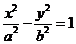
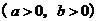 的离心率为
的离心率为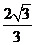 ,左、右焦点分别为
,左、右焦点分别为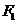 、
、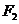 ,在双曲线
,在双曲线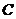 上有一点
上有一点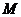 ,使
,使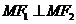 ,且
,且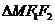 的面积为
的面积为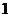 .
.
(1)求双曲线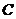 的方程;
的方程;
(2)过点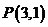 的动直线
的动直线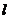 与双曲线
与双曲线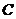 的左、右两支分别相交于两点
的左、右两支分别相交于两点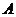 、
、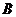 ,在线段
,在线段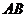 上取异于
上取异于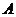 、
、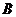 的点
的点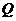 ,满足
,满足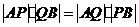 .证明:点
.证明:点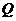 总在某定直线上.
总在某定直线上.
(1)解:∵双曲线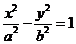
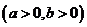 的离心率为
的离心率为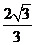 ,
,
∴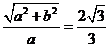 .即
.即 . ① (3分)
. ① (3分)
∵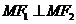 ,且
,且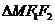 的面积为1.
的面积为1.
∴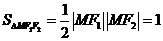 ,即
,即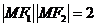 .
.
∵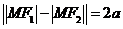 ,
,
∴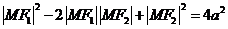 .
.
∴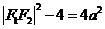 .
.
∴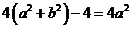 ,∴
,∴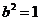 . ② (6分)
. ② (6分)
将②代入①,得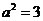 .
.
∴双曲线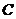 的方程为
的方程为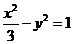 . (8分)
. (8分)
(2)设点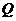 ,
,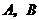 的坐标分别为
的坐标分别为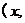
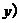 ,
,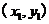 ,
,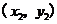 ,且
,且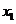 <
<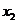 <3,
<3,
∵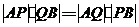 ,
,
∴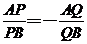 ,即
,即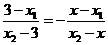 ,
,
即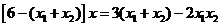 . ③ (10分)
. ③ (10分)
设直线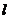 的方程为
的方程为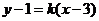 , ④
, ④
将④代入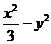 =1中整理,得
=1中整理,得
(1-3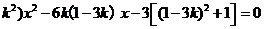 .
.
依题意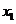 ,
,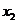 是上述方程的两个根,且
是上述方程的两个根,且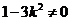 ,
,
∴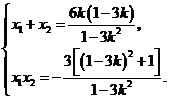 ⑤
⑤
将⑤代入③整理,得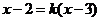 . ⑥
(12分)
. ⑥
(12分)
由④、⑥消去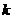 得
得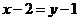 ,这就是点
,这就是点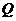 所在的直线方程. (14分)
所在的直线方程. (14分)
∴点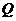 (
(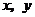 )总在定直线
)总在定直线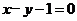 上.
上.
21.(本小题满分12分)
已知函数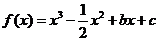 ,且
,且 在
在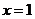 处取得极值
处取得极值
(1)求实数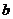 的值;
的值;
(2)若当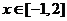 时,
时,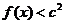 恒成立,求
恒成立,求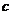 的取值范围;
的取值范围;
(3)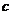 为何值时,曲线
为何值时,曲线 与
与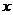 轴仅有一个交点.
轴仅有一个交点.
解:(1)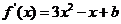 ,
,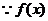 在
在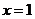 处取得极值,
处取得极值,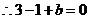 ,即
,即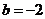 (3分)
(3分)
(2)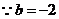 ,
,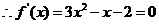 得
得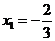 ,
,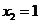
当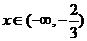 时,
时,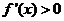 ,函数
,函数 单调递增;
单调递增;
当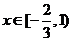 时,
时,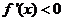 ,函数
,函数 单调递减;
单调递减;
当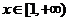 时,单调递增; (6分)
时,单调递增; (6分)
而当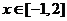 时,
时,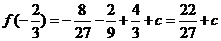 ,
,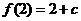
∴在闭区间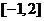 上,
上,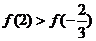 ,
,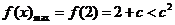
∴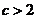 或
或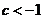 (8分)
(8分)
(3)由(1),(2)可知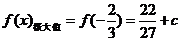 ,
,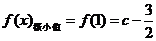
当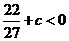 或
或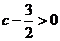 ,即
,即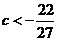 或
或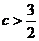 时
时 与
与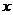 轴仅有一个交点(12分)
轴仅有一个交点(12分)
20. (本题满分12分)
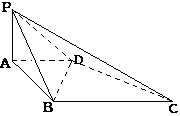 已知四边形ABCD为直角梯形,AD∥BC,∠ABC=90°,PA⊥平面AC,且PA=AD=AB=1,BC=2
已知四边形ABCD为直角梯形,AD∥BC,∠ABC=90°,PA⊥平面AC,且PA=AD=AB=1,BC=2
(1)求异面直线PC与BD所成角的余弦值的大小;
(2)求证:二面角B-PC-D为直二面角.
解: (1)因为PA⊥平面AC,AB⊥BC,∴PB⊥BC,即∠PBC=90°,由勾股定理得PB=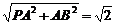 .∴PC=
.∴PC=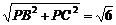 .
.
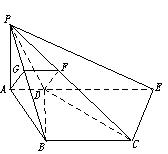
如图,过点C作CE∥BD交AD的延长线于E,连结PE,则PC与BD所成的角为∠PCE或它的补角.
∵CE=BD=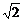 ,且PE=
,且PE=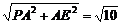
∴由余弦定理得cosPCE=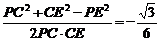
∴PC与BD所成角的余弦值为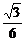 .
(6分)
.
(6分)
(2)证明:设PB、PC中点分别为G、F,连结FG、AG、DF,则GF∥BC∥AD,且GF=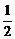 BC=1=AD,从而四边形ADFG为平行四边形,
BC=1=AD,从而四边形ADFG为平行四边形,
又AD⊥平面PAB,∴AD⊥AG,即ADFG为矩形,DF⊥FG.
在△PCD中,PD=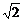 ,CD=
,CD=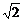 ,F为BC中点,∴DF⊥PC
,F为BC中点,∴DF⊥PC
从而DF⊥平面PBC,故平面PDC⊥平面PBC,即二面角B-PC-D为直二面角(12分)
19.(本小题满分12分)
已知数列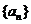 ,
,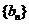 分别满足
分别满足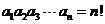 ,
, .
.
(Ⅰ)求数列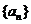 ,
,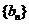 的通项公式;
的通项公式;
(Ⅱ)若数列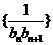 的前
的前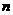 项和为
项和为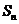 ,求
,求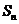 .
.
解:(Ⅰ)当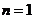 时,
时,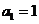 ;
;
由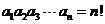 可得
可得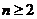 时,
时,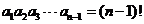 ,可得
,可得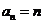 ,且
,且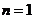 时成立;
时成立;
由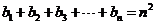 ,得
,得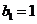 。
。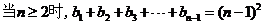 ,
,
由此可得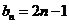 ,且
,且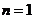 时成立;
(6分)
时成立;
(6分)
故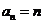 ,
,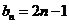
(Ⅱ)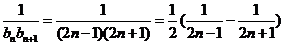
故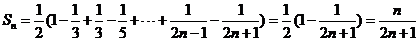 (12分)
(12分)
18.(本小题满分12分)
有A、B、C、D四个城市,它们都有一个著名的旅游景点,依次记为a、b、c、d,现把A、B、C、D和a、b、c、d分别写成左、右两列,今有一名旅游爱好者随机用4条线段把左、右全部连接起来,构成“一一对应”,已知连对一根线得2分,连错一根得0分。
(Ⅰ)求连对2根线的概率;
(Ⅱ)求该旅游爱好者得分的分布列和数学期望。
解:(Ⅰ)设连对线的个数为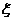 .依题意
.依题意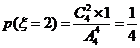 . (3分)
. (3分)
(Ⅱ)设得分为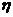 , 则
, 则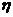 =0,2,4,8,
=0,2,4,8,
则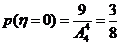 ,
,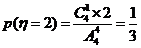 ,
,
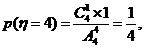
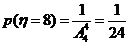 .
.
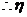 的分布列
的分布列
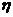 |
0 |
2 |
4 |
8 |
|
P |
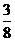 |
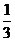 |
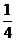 |
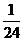 |
(9分)
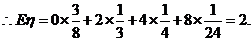 (12分)
(12分)
17.(本小题满分12分)
在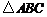 中,
中,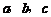 分别是三个内角
分别是三个内角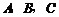 的对边.若
的对边.若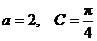 ,
,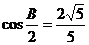 ,
,
(1)求角B的余弦值; (2)求
(2)求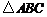 的面积
的面积 .
.
解: (1)由题意,得cosB = 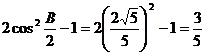 (6分)
(6分)
(2)由(1)易得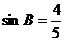 , 由C = ,
, 由C = ,
得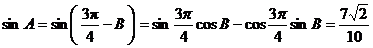 , (8分)
, (8分)
由正弦定理得 
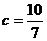 (10分)
(10分)
∴ 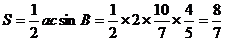 ,故△ABC的面积是
,故△ABC的面积是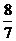 . (12分)
. (12分)
16.对于非零向量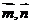 ,定义运算“#”:
,定义运算“#”:
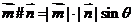 ,其中
,其中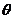 为
为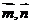 的夹角.有两两不共线的三个向量
的夹角.有两两不共线的三个向量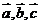 ,下列结论:
,下列结论:
①若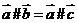 ,则
,则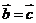 ;
; 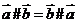 ;③若
;③若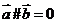 ,则
,则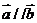 ;④
;④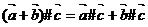 ;⑤
;⑤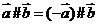 .其中所有正确结论的序号是_________
.其中所有正确结论的序号是_________
答案:②③⑤ 若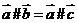 ,则
,则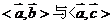 可以相等与可以互补,①错误;当
可以相等与可以互补,①错误;当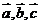 都为单位向量,且
都为单位向量,且 反向,
反向, 都与
都与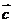 垂直时,
垂直时,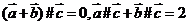 ,④错误。
,④错误。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com