
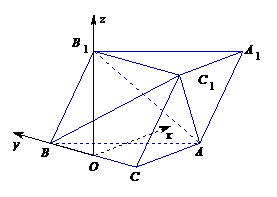
19.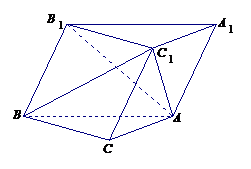 (本小题满分12分)如图,斜三棱柱
(本小题满分12分)如图,斜三棱柱 的底面是直角三角形,
的底面是直角三角形, ,点
,点 在底面
在底面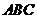 上的射影恰好是
上的射影恰好是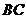 的中点,且
的中点,且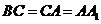 .
.
(Ⅰ)求证:平面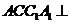 平面
平面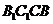 ;
;
(Ⅱ)求证: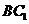
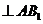 ;
;
(Ⅲ)求二面角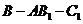 的大小.
的大小.
解:(Ⅰ)证明:设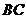 的中点为
的中点为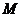 .
.
在斜三棱柱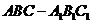 中,点
中,点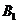 在底面
在底面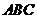 上的射影恰好是
上的射影恰好是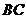 的中点,
的中点,

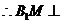 平面ABC.
……………………1分
平面ABC.
……………………1分
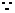
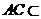 平面
平面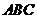 ,
,
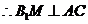 .
……………………2分
.
……………………2分
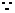
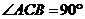 ,
,
∴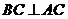 .
.
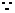
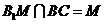 ,
,
∴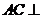 平面
平面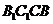 .
……………………4分
.
……………………4分
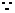
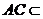 平面
平面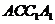 ,
,
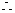 平面
平面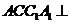 平面
平面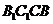 .
………………………………………5分
.
………………………………………5分
解法一:(Ⅱ)连接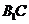 ,
,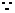
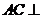 平面
平面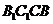 ,
,
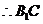 是直线
是直线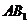 在平面
在平面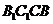 上的射影.
………………………………………5分
上的射影.
………………………………………5分
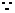
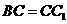 ,
,
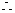 四边形
四边形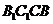 是菱形.
是菱形.
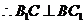 .
………………………………………7分
.
………………………………………7分
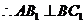 .
………………………………………9分
.
………………………………………9分
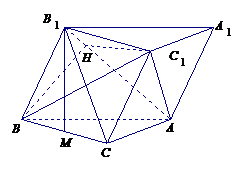 (Ⅲ)过点
(Ⅲ)过点 作
作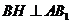 交
交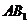 于点
于点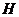 ,连接
,连接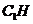 .
.
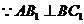 ,
,
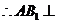 平面
平面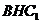 .
.
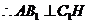 .
.
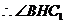 是二面角
是二面角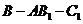 的平面角. ……………11分
的平面角. ……………11分
设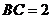 ,则
,则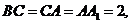
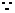
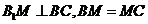 ,
,
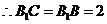 .
.
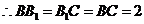 .
.
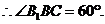
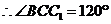 .
.
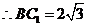 .
.
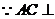 平面
平面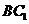 ,
,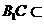 平面
平面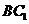 ,
,
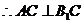 .
.
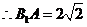 .
.
在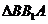 中,可求
中,可求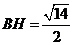 .
.
∵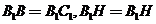 ,∴
,∴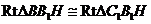 .
.
∴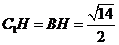 .
.
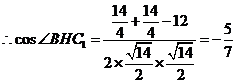 .
………………………………………13分
.
………………………………………13分
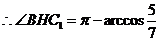 .
.
∴二面角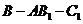 的大小为
的大小为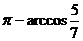 .
………………………………………14分
.
………………………………………14分
 解法二:(Ⅱ)因为点
解法二:(Ⅱ)因为点 在底面
在底面 上的射影是
上的射影是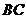 的中点,设
的中点,设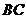 的中点为
的中点为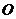 ,则
,则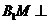 平面ABC.以
平面ABC.以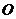 为原点,过
为原点,过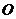 平行于
平行于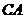 的直线为
的直线为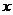 轴,
轴,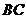 所在直线为
所在直线为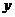 轴,
轴,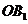 所在直线为
所在直线为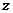 轴,建立如图所示的空间直角坐标系.
轴,建立如图所示的空间直角坐标系.
设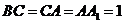 ,由题意可知,
,由题意可知,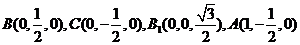 .
.
设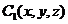 ,由
,由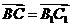 ,得
,得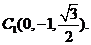
………………………………………7分
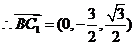 .
.
又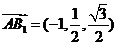 .
.
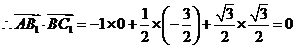 .
.
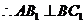 .
………………………………………9分
.
………………………………………9分
(Ⅲ)设平面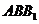 的法向量为
的法向量为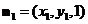 .
.
则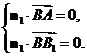
∴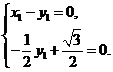
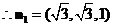 .
.
设平面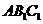 的法向量为
的法向量为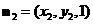 .则
.则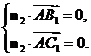
∴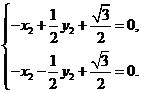
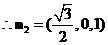 .
………………………………………12分
.
………………………………………12分
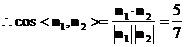 .
………………………………………13分
.
………………………………………13分
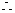 二面角
二面角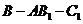 的大小为
的大小为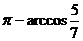 .
………………………………………14分
.
………………………………………14分
18.(本小题满分12分)在今年甲感流行期间,某市检测部门决定对全市学校教室的空气质量进行检测。空气质量分为A、B、C三级. 每间教室的检测方式如下:分别在同一天的上、下午各进行一次检测,若两次检测中有C级或两次都是B级,则该教室的空气质量不合格. 设各教室的空气质量相互独立,且每次检测的结果也相互独立. 根据多次抽检结果,一间教室一次检测空气质量为A、B、C三级的频率依次为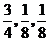 .
.
(Ⅰ)在该市的教室中任取一间,估计该间教室的空气质量合格的概率;
(Ⅱ)如果对该市某中学高三年级的4间教室进行检测,记检测空气质量合格的教室间数为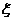 ,根据(Ⅰ)中的计算结果,求
,根据(Ⅰ)中的计算结果,求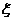 的分布列及期望.
的分布列及期望.
解:(Ⅰ)该间教室两次检测中,空气质量均为A级的概率为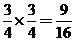 .………………………………2分
.………………………………2分
该间教室两次检测中,空气质量一次为A级,另一次为B级的概率为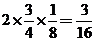 .
.
…………………………………4分
设“该间教室的空气质量合格”为事件E.则 …………………………………5分
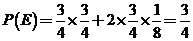 .
…………………………………6分
.
…………………………………6分
答:估计该间教室的空气质量合格的概率为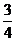 .
.
(Ⅱ)由题意可知,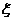 的取值为0,1,2,3,4.
…………………………………7分
的取值为0,1,2,3,4.
…………………………………7分
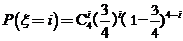
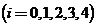 .
.
随机变量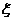 的分布列为:
的分布列为:
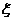 |
0 |
1 |
2 |
3 |
4 |
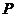 |
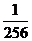 |
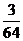 |
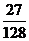 |
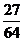 |
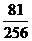 |
…………………………………11分
解法一:
∴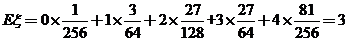 . …………………………………12分
. …………………………………12分
解法二: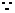
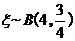 ,
,
∴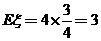 .
……………………12分
.
……………………12分
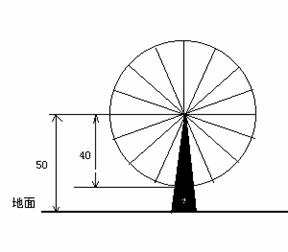
17.(本小题满分12分)如图,游乐场中的摩天轮做匀速转动,每6min转一圈,其中心点O距地面的高度为50m,半径为40m。若你从最低点处登上摩天轮, 且以你登上摩天轮时开始计时。当你登上摩天轮2min时,你的朋友也在摩天轮最低点处登上摩天轮。
(Ⅰ)求出你与地面的距离y(m)与时间t(min)的函数解析式;
 (Ⅱ)当你距地面30m时,用了多少时间?
(Ⅱ)当你距地面30m时,用了多少时间?
(Ⅲ)你的朋友登上摩天轮多长时间后,你们俩与地面距离相等?
解:(Ⅰ)设经过时间t,你在摩天轮上所经过的弧对应的圆心角为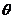 ,则
,则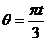 ,
,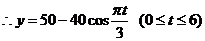 ……4分
……4分
(Ⅱ)由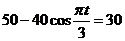 ,得
,得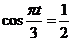 。
。
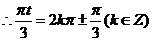 ,
,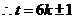 , ……6分
, ……6分
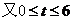 ,
,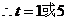 。
。
所以当你距地面30m时,用了1min或5min。……8分
(Ⅲ)设你登上摩天轮tmin后,你的朋友与地面的距离为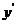 ,
,
则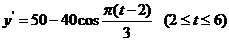 , ……10分
, ……10分
由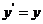 ,得
,得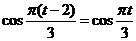 ,
,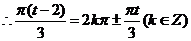 ,
,
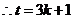 ,
,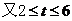 ,
,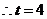 。……11分
。……11分
所以你的朋友登上摩天轮2min后,你们俩与地面距离相等. ……12分
16.下图展示了一个由区间(0,1)到实数集R的映射过程:区间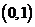 中的实数m对应数轴上的点M,如图1;将线段
中的实数m对应数轴上的点M,如图1;将线段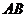 围成一个圆,使两端点A、B恰好重合,如图2;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为
围成一个圆,使两端点A、B恰好重合,如图2;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为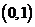 ,如图3.图3中直线
,如图3.图3中直线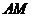 与x轴交于点
与x轴交于点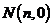 ,则m的象就是n,记作
,则m的象就是n,记作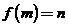 .
.

下列说法中正确命题的序号是 .(填出所有正确命题的序号)
①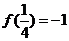 ; ②
; ②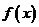 是奇函数; ③
是奇函数; ③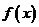 在定义域上单调递增;
④
在定义域上单调递增;
④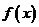 的图象关于点
的图象关于点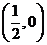 对称.
对称.
答案:①③④。
15.某校为了配合全市创建“低碳示范城”的活动之一,决定将学校景观道上的一排12个路灯,每晚只开其中的4个。要求这4盏灯中,相邻的至少相隔两个不开的路灯,则不同的亮灯方法共有 ______种(用数字作答).
答案:15。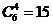
14.若x,y是正数,则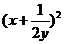 +
+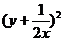 的最小值是 _________
的最小值是 _________
答案:4。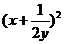 +
+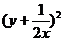
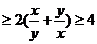 ,当且仅当
,当且仅当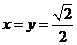 时取等号。
时取等号。
13. 在约束条件: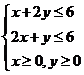 下,目标函数
下,目标函数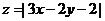 的最大值是
。
的最大值是
。
答案:8。在约束条件下,求得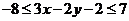 。
。
12. 已知O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足
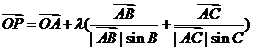 ,
,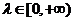 ,则点P的轨迹一定通
,则点P的轨迹一定通
过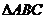 的( )
的( )
A.重心 B.垂心 C.内心 D.外心
答案:A。已知条件等价于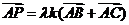 ,
,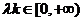 ,显然P的轨迹一定通过
,显然P的轨迹一定通过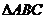 的重心。
的重心。
11. 如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则表上数字标签:
如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则表上数字标签:
原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,
点(-1,-1)处标4,点(-1,0)标5,点(-1,1)处标6,点(0,1)
处标7,以此类推,则标签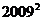 的格点的坐标为( )
的格点的坐标为( )
A.(1005,1004) B.(1004.1003) C.(2009,2008) D.(2008,2007)
答案:A。由图像可得标签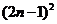 的格点的坐标为
的格点的坐标为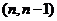 ,
,
∵2009是第1005个奇数,∴标签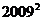 的格点的坐标为(1005,1004) 。
的格点的坐标为(1005,1004) 。
10.设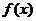 是
是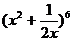 展开式的中间项,若
展开式的中间项,若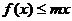 在区间
在区间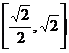 上恒成立,则实数
上恒成立,则实数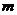 的取值范围是( )
的取值范围是( )
A.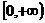 B.
B.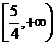 C.
C. 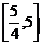 D.
D.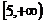
答案:D。∵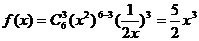 ,∴
,∴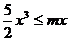 在区间
在区间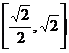 上恒成立,即
上恒成立,即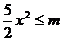 在区间
在区间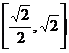 上恒成立,∴
上恒成立,∴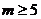 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com