
7.在数列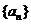 中,如果存在非零常数
中,如果存在非零常数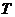 ,使得
,使得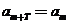 对于任意正整数
对于任意正整数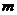 均成立,那么就称数列
均成立,那么就称数列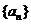 为以
为以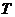 为周期的周期数列.已知数列
为周期的周期数列.已知数列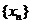 满足
满足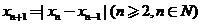 ,如果
,如果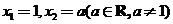 ,当数列
,当数列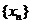 的周期最小时,该数列前
的周期最小时,该数列前 项的和是( ).
项的和是( ).
A.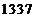 B.
B.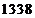 C.
C.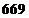 D.
D.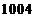
6.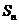 是等差数列
是等差数列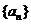 的前
的前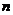 项和,若
项和,若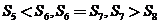 ,则下列说法错误的是( ).
,则下列说法错误的是( ).
A.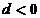 B.
B.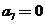 C.
C.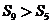 D.
D.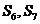 均为
均为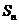 的最大值
的最大值
5.设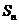 是等差数列
是等差数列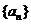 的前
的前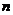 项和,且
项和,且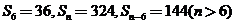 ,则
,则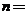 ( ).
( ).
A.9 B.36 C.17 D.18
4.已知等差数列共有 项,其中奇数项的和是
项,其中奇数项的和是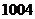 ,偶数项的和是
,偶数项的和是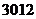 ,则其公差是( ).
,则其公差是( ).
A.1 B.2 C.3 D.4
3.若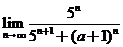 存在,则实数
存在,则实数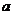 的取值范围是( ).
的取值范围是( ).
A.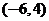 B.
B.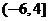 C.
C.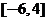 D.
D.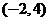
2.已知等差数列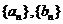 的前
的前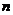 项和分别为
项和分别为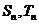 ,且
,且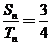 ,则
,则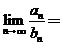 ( ).
( ).
A.1 B.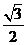 C.
C.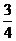 D.
D.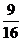
1.在半径为1的圆内作内接正三角形,然后在所得正三角形内作内切圆,接着在第2个圆内再作内接正三角形,如此无限作下去,则所有这些圆的面积之和(即前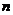 项和
项和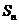 的极限
的极限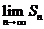 )是( ).
)是( ).
A.
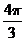 B.
B. 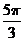 C.
C. 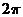 D.不存在
D.不存在
18. (13分)根据下面的要求,求满足1+2+3+…+n > 500的最小的自然数n.
(1)右面是解决该问题的一个程序,但有3处错误,请找
出错误并予以更正;
(2)画出执行该问题的程序框图。
|
西安铁一中09-10学年高二上学期第一次月考
17.(12分)(理科题)在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.
(1)求取出的两个球上标号为相邻整数的概率;
(2)求取出的两个球上标号之和能被3整除的概率.
(文科题)给出五个数字1,2,3,4,5;
(1)用这五个数字能组成多少个无重复数字的四位偶数?
(2)用这些数字作为点的坐标,能得到多少个不同的点(数字可以重复用) ?
16.(理科题) 甲、乙两人玩数字游戏,先由甲心中任想一个数字记为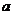 ,再由乙猜甲刚才想的数字,把乙想的数字记为
,再由乙猜甲刚才想的数字,把乙想的数字记为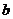 ,且
,且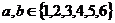 ,若
,若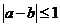 ,则称“甲乙心有灵犀”,
现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________.
,则称“甲乙心有灵犀”,
现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________.
(文科题)下列说法中正确的有________
①刻画一组数据集中趋势的统计量有极差、方差、标准差等;刻画一组数据离散程度统计量有平均数、中位数、众数等.
②解决某类问题的算法不一定是唯一的,但执行后一定得到确定的结果.
③有10个阄,其中一个代表奖品,10个人按顺序依次抓阄来决定奖品的归属,则摸奖的顺序对中奖率没有影响.
④用样本频率分布估计总体频率分布的过程中,总体容量越大,估计越精确.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com