22、解：(1)法一：作MM₁⊥于M₁，

NN₁⊥于N₁，则，

又由椭圆的第二定义有

∴

∴∠KMM₁=∠KNN₁，即∠MKF=∠NKF，

∴KF平分∠MKN………………………………5分

法二：设直线MN的方程为.

设M、N的坐标分别为, 由

∴

设KM和KN的斜率分别为，显然只需证即可.

∵　 ∴

而

即 得证.

(2)由A，M，P三点共线可求出P点的坐标为

由A，N，Q三点共线可求出Q点坐标为，……………………7分

设直线MN的方程为.由

∴…………………………………………9分

则：

……………………………………11分

又直线MN的倾斜角为，则，∴

∴时，………………………………………………………………12分

21、解：∵f¢ (x)＝4a₀x³+3a₁x²+2a₂x+a₃为偶函数，∴ f ¢(-x) = f ¢(x),

∴　 -4a₀x³ +3a₁x² -2a₂x + a₃ = 4a₀x³+3a₁x² +2a₂x + a₃,

∴　 4a₀x³ + 2a₂x =0对一切x Î R恒成立，

∴　 a₀＝a₂＝0，∴f (x)＝a₁x³+a₃x　 　

又当x＝－时，f (x)取得极大值

∴ 解得∴f (x)＝x³－x，f¢ (x)＝2x²－1 4分

⑵解：设所求两点的横坐标为x₁、x₂ (x₁ < x₂)，则(2x₁²－1)(2x₂²－1)＝－1

又∵x₁，x₂∈[－1，1]，∴2x₁²－1∈[－1，1]，2x₂²－1∈[－1，1]

∴2x₁²－1，2x₂²－1中有一个为1，一个为－1，　　

∴或 ，∴所求的两点为(0，0)与(1，－)或(0，0)与(－1，)。

⑶证明：易知sin x∈[－1，1]，cos x∈[－1，1]。

当0< x < 时，f ¢ (x) < 0；当 < x < 1时，f ¢ (x)>0。

∴f (x)在[0，]为减函数，在[，1]上为增函数，

又f (0)＝0，f ()＝－ ，f (1)＝－，而f (x)在[－1，1]上为奇函数，

∴f (x)在[－1，1]上最大值为，最小值为－，即 | f (x) | ≤ ,

∴| f (sin x) | ≤ ，| f (cos x)| ≤ ， ∴| f (sin x)－f (cos x)| ≤ | f (sin x)|+| f (cos x) | ≤

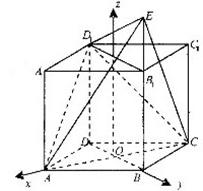
20、解：(Ⅰ)设与交于，如图所示建立空间直角坐标系，设爿，

则设

则

平面

即　 　……………………3分

设平面的法向量为……………………5分

则由 得 　　令

平面的一个法向量为

又平面的法向量为

二面角大小为………………………………………………………………7分

(Ⅱ)设得

　…………10分

面

存在点使面此时……………12分

19、(1)设盒中有n张“世博会会徽”卡，由题意得,解得：n=5,所以，有海宝卡4张，获奖概率为

(2)若有3人获奖，则=

18、解：(1)设等差数列的公差为d，由，得

，…………………………………………2分

则，，中，…………………3分

则，………………………………………………………4分

当时，，……………………6分

则=

=………………………………………………………………8分

(3)

=

==…………………………………10分

即的最大值为-1……………………………………12分

17、解①

cos<>=cos==cos　　　

②　

13、　 14、 15、 1　 16

21、设定义在R上的函数 ，当时，f (x)取得极大值，并且函数y＝f¢ (x)的图象关于y轴对称。

(1)求f (x)的表达式；

(2)试在函数f (x)的图象上求两点，使以这两点为切点的切线互相垂直，且切点的横坐标都在区间[－1 ，1]上；

(3)求证：|f (sin x)－f (cos x) | ≤ 　 (x∈R)．

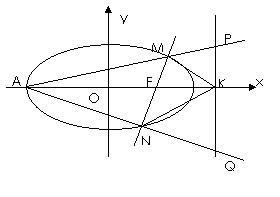22如图，已知椭圆的右焦点为F，过F的直线(非x轴)交椭圆于M、N两点，右准线交x轴于点K，左顶点为A.

(1)求证：KF平分∠MKN；

(2)直线AM、AN分别交准线于点P、Q，

设直线MN的倾斜角为，试用表示线段

PQ的长度|PQ |，并求|PQ |的最小值.

一摸考试文科数学答案

A:1-5: ADBBA　 6-10:CDCAA　 11-12: DB

20、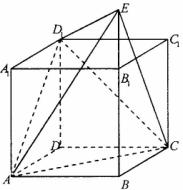直四棱柱中，底面为菱形，且为延长线上的一点，面。

　　 (1)求二面角的大小；

　　 (2)在上是否存在一点，使面?若存在，求的值，不存在，说明理由。

19、某单位举办2010年上海世博会知识宣传活动，进行现场抽奖.盒中装有9张大小相同的精美卡片，卡片上分别印有“世博会会徽”或“海宝”(世博会吉祥物)图案；抽奖规则是：参加者从盒中抽取卡片两张，若抽到两张都是“海宝”卡即可获奖，否则，均为不获奖.卡片用后放回盒子，下一位参加者继续重复进行.

(1)活动开始后，一位参加者问：盒中有几张“海宝”卡？主持人答：我只知道，从盒中抽取两张都是“世博会会徽“卡的概率是，求抽奖者获奖的概率；

(2)现有甲、乙、丙、丁四人依次抽奖，用表示获奖的人数，求.