083]. 解：(1)B(1，)

(2)设抛物线的解析式为y=ax(x+a)，代入点B(1, )，得，

因此

(3)如图，抛物线的对称轴是直线x=-1，当点C位于对称轴与线段AB的交点时，△BOC的周长最小.

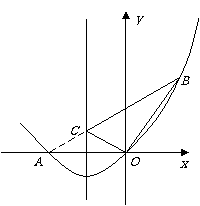设直线AB为y=kx+b.所以，

因此直线AB为，

当x=－1时，，

因此点C的坐标为(－1，).

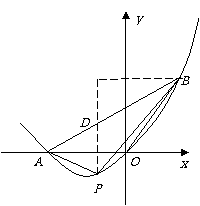(4)如图，过P作y轴的平行线交AB于D.

当x=－时，△PAB的面积的最大值为，此时.

082](09上海)略

081]解：(1)(0，－3)，b＝－，c＝－3．···························································· 3分

(2)由(1)，得y＝x²－x－3，它与x轴交于A，B两点，得B(4，0)．

∴OB＝4，又∵OC＝3，∴BC＝5．

由题意，得△BHP∽△BOC，

∵OC∶OB∶BC＝3∶4∶5，

∴HP∶HB∶BP＝3∶4∶5，

∵PB＝5t，∴HB＝4t，HP＝3t．

∴OH＝OB－HB＝4－4t．

由y＝x－3与x轴交于点Q，得Q(4t，0)．

∴OQ＝4t．··························································································· 4分

①当H在Q、B之间时，

QH＝OH－OQ

＝(4－4t)－4t＝4－8t．································································ 5分

②当H在O、Q之间时，

QH＝OQ－OH

＝4t－(4－4t)＝8t－4．································································ 6分

综合①，②得QH＝｜4－8t｜；································································ 6分

(3)存在t的值，使以P、H、Q为顶点的三角形与△COQ相似．···················· 7分

①当H在Q、B之间时，QH＝4－8t，

若△QHP∽△COQ，则QH∶CO＝HP∶OQ，得＝，

∴t＝．···························································································· 7分

若△PHQ∽△COQ，则PH∶CO＝HQ∶OQ，得＝，

即t²+2t－1＝0．

∴t₁＝－1，t₂＝－－1(舍去)．················································· 8分

②当H在O、Q之间时，QH＝8t－4．

若△QHP∽△COQ，则QH∶CO＝HP∶OQ，得＝，

∴t＝．···························································································· 9分

若△PHQ∽△COQ，则PH∶CO＝HQ∶OQ，得＝，

即t²－2t+1＝0．

∴t₁＝t₂＝1(舍去)．·········································································· 10分

综上所述，存在的值，t₁＝－1，t₂＝，t₃＝．························ 10分

附加题：解：(1)8；···································································································· 5分

(2)2．·································································································· 10分

090]如图(9)-1，抛物线经过A(，0)，C(3，)两点，与轴交于点D，与轴交于另一点B．

(1)求此抛物线的解析式；

(2)若直线将四边形ABCD面积二等分，求的值；

(3)如图(9)-2，过点E(1，1)作EF⊥轴于点F，将△AEF绕平面内某点旋转180°得△MNQ(点M、N、Q分别与点A、E、F对应)，使点M、N在抛物线上，作MG⊥轴于点G，若线段MG︰AG＝1︰2，求点M，N的坐标．

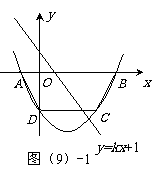
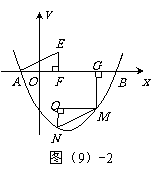
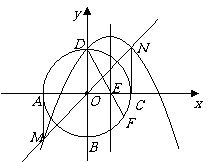
089]如图，在平面直角坐标系中，半径为1的圆的圆心在坐标原点，且与两坐标轴分别交于四点．抛物线与轴交于点，与直线交于点，且分别与圆相切于点和点．

(1)求抛物线的解析式；

(2)抛物线的对称轴交轴于点，连结，并延长交圆于，求的长．

(3)过点作圆的切线交的延长线于点，判断点是否在抛物线上，说明理由．

088]如图所示，已知在直角梯形中，轴于点．动点从点出发，沿轴正方向以每秒1个单位长度的速度移动．过点作垂直于直线，垂足为．设点移动的时间为秒()，与直角梯形重叠部分的面积为．

(1)求经过三点的抛物线解析式；

(2)求与的函数关系式；

(3)将绕着点顺时针旋转，是否存在，使得的顶点或在抛物线上？若存在，直接写出的值；若不存在，请说明理由．

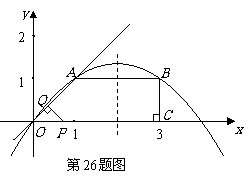
087]如图，已知抛物线y＝x²+bx+c经过矩形ABCD的两个顶点A、B，AB平行于x轴，对角线BD与抛物线交于点P，点A的坐标为(0，2)，AB＝4．

(1)求抛物线的解析式；

(2)若S_△APO＝，求矩形ABCD的面积．

086]如图，以BC为直径的⊙O交△CFB的边CF于点A，BM平分

∠ABC交AC于点M，AD⊥BC于点D，AD交BM于点N，ME⊥BC于点E，AB²=AF·AC，cos∠ABD=，AD=12．

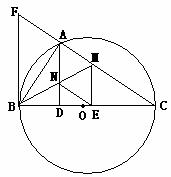⑴求证：△ANM≌△ENM；

⑵求证：FB是⊙O的切线；

⑶证明四边形AMEN是菱形，并求该菱形的面积S．

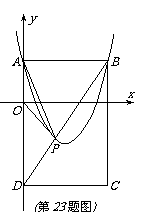
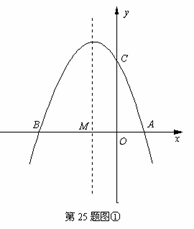
085]如图①， 已知抛物线(a≠0)与轴交于点A(1，0)和点B (－3，0)，与y轴交于点C．

(1) 求抛物线的解析式；

(2) 设抛物线的对称轴与轴交于点M ，问在对称轴上是否存在点P，使△CMP为等腰三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．

(3) 如图②，若点E为第二象限抛物线上一动点，连接BE、CE，求四边形BOCE面积的最大值，并求此时E点的坐标．

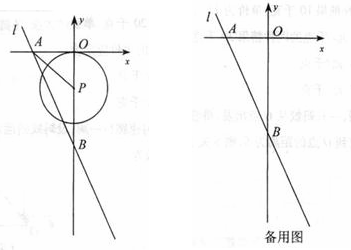
084]如图，在平面直角坐标系中，直线l：y=－2x－8分别与x轴，y轴相交于A，B两点，点P(0，k)是y轴的负半轴上的一个动点，以P为圆心，3为半径作⊙P.

(1)连结PA，若PA=PB，试判断⊙P与x轴的位置关系，并说明理由；

(2)当k为何值时，以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形？