1. 已知全集U={1,2,3,4,5,6,7,8} P={3,4,5}　 Q={1,3,6} 那么集合{2,7,8}是(　 )

A. P∪Q　　 B. P∩Q　　 C. C_uP∪C_uQ　　　 D.C_uP∩C_uQ

10、[解] (1)由得，

由与两式相除，有：

，………………….4分

又通过知：，

则，，

则．………………….8分

(2)由，得到．………………….10分

由….14

9、[解](1)令；再令

　 (2)　　　 令代入已知得：

＃

　 (3)。

8、解　 (1)在Rt△ADC中，AD=8，CD=6，

则AC=10，．………………2分

又∵，AB=13，

∴． …………………………4分

∵，∴． ………………………………5分

∴．…………………………………8分

(2)，，，……………………………………11分

则，∴．……………………14分

7、证明：(Ⅰ) 直棱柱中，BB₁⊥平面ABCD，BB₁⊥AC．

又∠BAD＝∠ADC＝90°，，

∴，∠CAB＝45°，∴， BC⊥AC．

又，平面BB₁C₁C， AC⊥平面BB₁C₁C．　

(Ⅱ)存在点P，P为A₁B₁的中点．

证明：由P为A₁B₁的中点，有PB₁‖AB，且PB₁＝AB．

又∵DC‖AB，DC＝AB，DC ∥PB₁，且DC＝ PB₁，

∴DC PB₁为平行四边形，从而CB₁∥DP．

又CB₁面ACB₁，DP 面ACB₁，DP‖面ACB₁．

同理，DP‖面BCB₁．

10、设的内角所对的边长分别为，且，．

(Ⅰ)求和边长；

(Ⅱ)若的面积，求的值．

9、是上的函数，对于任意和实数，都有，

且。 (1)求的值； (2)令，求证：为等差数列；　　

(3)求的通项公式。

8、如图，在四边形ABCD中，AD=8，CD=6，AB=13，∠ADC=90°，且．

(1)求sin∠BAD的值；

(2)设△ABD的面积为S_△ABD，△BCD的面积为

S_△BCD，求的值．

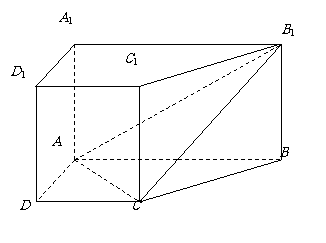
7、直棱柱中，底面ABCD是直角梯形，

∠BAD＝∠ADC＝90°，．

(Ⅰ)求证：AC⊥平面BB₁C₁C；

(Ⅱ)在A₁B₁上是否存一点P，使得DP与平面BCB₁与平面ACB₁都平行？证明你的结论．

9．材料一　 小明在班级中学习成绩不理想，他看到同学买了一双名牌运动鞋非常羡慕。小明的父母收入不高，经济条件有限，他就问同学借钱也买了一双。许多同学都投来羡慕的眼光，小明觉得很有面子，有了自尊。

材料二　 “人不可有傲气，但不可无傲骨。”---徐悲鸿

请回答：

(1)小明的做法是为自己赢得了自尊吗?为什么?

(2)如何理解材料二中的“傲气”和“傲骨”?

(3)从两则材料的回答中我们可以悟出一个什么道理?