23. 江苏省羽毛球A队与B队进行对抗比赛，在每局比赛中A队获胜的概率都是。

(1)若比赛6局，且，求A队至少获胜4局的概率；

(2)若采用“五局三胜”制，求A队获胜时的比赛局数的分布列和数学期望。

22.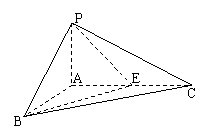如图所示，在三棱锥P－ABC中，PA⊥平面ABC，， E为AC的中点。

(1)求异面直线BE与PC所成角的余弦值；

(2)求二面角P－BE－C的平面角的余弦值。

21.[选做题]在A，B，C，D四小题中只能选做2题，每小题10分，共计20分。解答时应写出文字说明、证明过程或演算步骤。

A．选修4-1：几何证明选讲

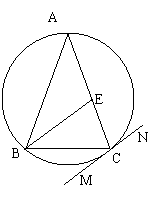如图，内接于圆，，直线切圆于点C，交于点E，若，求AE的长。

B．选修4-2：矩阵与变换

在直角坐标系中，已知的顶点坐标为。求在矩阵作用下变换所得到的图形的面积。

C．选修4-4：坐标系与参数方程

把参数方程(为参数)化为普通方程。

D．选修4-5：不等式选讲

已知为正数，且满足，求证：。

[必做题]第22题、第23题，每题10分，共计20分。解答时应写出文字说明、证明过程或演算步骤。

20.(本题满分16分)

在数列中，，，且()．

(Ⅰ)设()，证明是等比数列；

(Ⅱ)求数列的通项公式；

(Ⅲ)若是与的等差中项，求的值，并证明：对任意的，是与的等差中项．

江宁高级中学2010届高三12月调研测试理科数学附加试卷

(满分40分，考试时间30分钟)

19．(本题满分16分)

已知函数

(1)当时，求函数的单调区间和极值；

(2)若在上是单调增函数，求实数的取值范围。

18. (本题满分16分)

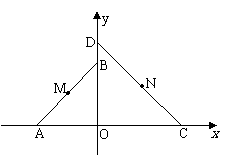
如图，在平面直角坐标系中，和为两等腰直角三角形，。设和的外接圆圆心分别为M，N。

(1)若⊙M与直线CD相切，求直线CD的方程；

(2)若直线AB截⊙N所得弦长为4，求⊙N的标准方程；

(3)是否存在这样的⊙N，使得⊙N上有且只有三个点到直线AB的距离为，若存在，求此时⊙N的标准方程；若不存在，说明理由。

17. (本题满分14分)

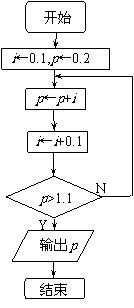
某旅游商品生产企业，2008年某商品生产的投入成本为1元/件，出厂价为流程图的输出结果元/件，年销售量为10 000件。此企业为适应市场需求，计划提高产品档次，适度增加投入成本。若每件投入成本增加的比例为，则出厂价相应提高的比例为，同时预计销售量增加的比例为。已知利润=(出厂价－投入成本)×年销售量。

(1)写出2009年预计的年利润与投入成本增加的比例的关系式；

(2)为使2009年的年利润比2008年有所增加，问：投入成本增加的比例应在什么范围内？

16.(本题满分14分)

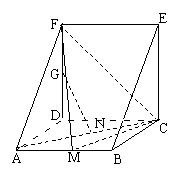
一个多面体的三视图和直观图分别如图所示，其中分别是的中点，是上的一动点。

(1)求证：；

(2)当时，在棱上确定一点，使得平面，并给出证明。

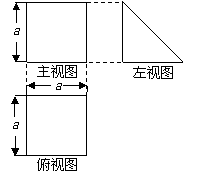
15.(本题满分14分)

△ABC中，角A的对边长等于2，向量，向量.

(1)求取得最大值时的角A的大小；

(2)在(1)的条件下，求△ABC面积的最大值.

14.考查下列一组不等式：

，，，……

将上述不等式在左右两端仍为两项和的情况下加以推广，使以上的不等式成为推广不等式的特例，则推广的不等式可以是　 　▲　　 。