1．　 书面作业：课本P₄₅ 习题1．3(A组) 第6、7、8题．

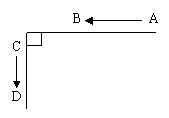提高作业：快艇和轮船分别从A地和C地同时开出，如下图，各沿箭头方向航行，快艇和轮船的速度分别是45 km/h和15 km/h，已知AC=150km，经过多少时间后，快艇和轮船之间的距离最短？

函数的单调性一般是先根据图象判断，再利用定义证明．画函数图象通常借助计算机，求函数的单调区间时必须要注意函数的定义域，单调性的证明一般分五步：

取 值 → 作 差 → 变 形 → 定 号 → 下结论

(二)典型例题

例1．(教材P₃₆例3)利用二次函数的性质确定函数的最大(小)值．

解：(略)

说明：对于具有实际背景的问题，首先要仔细审清题意，适当设出变量，建立适当的函数模型，然后利用二次函数的性质或利用图象确定函数的最大(小)值．

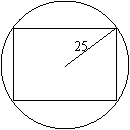巩固练习：如图，把截面半径为

25cm的圆形木头锯成矩形木料，

如果矩形一边长为x，面积为y

试将y表示成x的函数，并画出

函数的大致图象，并判断怎样锯

才能使得截面面积最大？

例2．(新题讲解)

旅 馆 定 价

　　　 一个星级旅馆有150个标准房，经过一段时间的经营，经理得到一些定价和住房率的数据如下：

欲使每天的的营业额最高，应如何定价？

解：根据已知数据，可假设该客房的最高价为160元，并假设在各价位之间，房价与住房率之间存在线性关系．

设为旅馆一天的客房总收入，为与房价160相比降低的房价，因此当房价为元时，住房率为，于是得

=150··．

由于≤1，可知0≤≤90．

因此问题转化为：当0≤≤90时，求的最大值的问题．

将的两边同除以一个常数0.75，得₁=－²+50+17600．

由于二次函数₁在=25时取得最大值，可知也在=25时取得最大值，此时房价定位应是160－25=135(元)，相应的住房率为67.5%，最大住房总收入为13668.75(元)．

所以该客房定价应为135元．(当然为了便于管理，定价140元也是比较合理的)

例3．(教材P₃₇例4)求函数在区间[2，6]上的最大值和最小值．

解：(略)

注意：利用函数的单调性求函数的最大(小)值的方法与格式．

巩固练习：(教材P₃₈练习4)　　

(一)函数最大(小)值定义

1．最大值

　　　 一般地，设函数y=f(x)的定义域为I，如果存在实数M满足：

　　　 (1)对于任意的x∈I，都有f(x)≤M；

　　　 (2)存在x₀∈I，使得f(x₀) = M

　　　 那么，称M是函数y=f(x)的最大值(Maximum Value)．

思考：仿照函数最大值的定义，给出函数y=f(x)的最小值(Minimum Value)的定义．(学生活动)

注意：

1 函数最大(小)首先应该是某一个函数值，即存在x₀∈I，使得f(x₀) = M；

2 函数最大(小)应该是所有函数值中最大(小)的，即对于任意的x∈I，都有f(x)≤M(f(x)≥M)．

　　　 2．利用函数单调性的判断函数的最大(小)值的方法

　　　 1 利用二次函数的性质(配方法)求函数的最大(小)值

　　　 2 利用图象求函数的最大(小)值

　　　 3 利用函数单调性的判断函数的最大(小)值

　　　 如果函数y=f(x)在区间[a，b]上单调递增，在区间[b，c]上单调递减则函数y=f(x)在x=b处有最大值f(b)；

如果函数y=f(x)在区间[a，b]上单调递减，在区间[b，c]上单调递增则函数y=f(x)在x=b处有最小值f(b)；

画出下列函数的图象，并根据图象解答下列问题：

1 说出y=f(x)的单调区间，以及在各单调区间上的单调性；

2 指出图象的最高点或最低点，并说明它能体现函数的什么特征？

(1)　　　　　　　　　　　 (2)

(3)　　　　　　　　 (4)　

3．　 课后思考：

已知是定义在R上的函数，

设，

1 试判断的奇偶性；

2 试判断的关系；

3 由此你能猜想得出什么样的结论，并说明理由．

2．补充作业：判断下列函数的奇偶性：

1 ；

2 ；

3 　()

4 　

1．　 书面作业：课本P₄₆ 习题1．3(A组) 第9、10题， B组第2题．

本节主要学习了函数的奇偶性，判断函数的奇偶性通常有两种方法，即定义法和图象法，用定义法判断函数的奇偶性时，必须注意首先判断函数的定义域是否关于原点对称．单调性与奇偶性的综合应用是本节的一个难点，需要学生结合函数的图象充分理解好单调性和奇偶性这两个性质．

(三)典型例题

1．判断函数的奇偶性

例1．(教材P₃₆例3)应用函数奇偶性定义说明两个观察思考中的四个函数的奇偶性．(本例由学生讨论，师生共同总结具体方法步骤)

解：(略)

总结：利用定义判断函数奇偶性的格式步骤：

1 首先确定函数的定义域，并判断其定义域是否关于原点对称；

2 确定f(－x)与f(x)的关系；

3 作出相应结论：

若f(－x) = f(x) 或 f(－x)－f(x) = 0，则f(x)是偶函数；

若f(－x) =－f(x) 或 f(－x)+f(x) = 0，则f(x)是奇函数．

巩固练习：(教材P₄₁例5)

例2．(教材P₄₆习题1．3 B组每1题)

解：(略)

说明：函数具有奇偶性的一个必要条件是，定义域关于原点对称，所以判断函数的奇偶性应应首先判断函数的定义域是否关于原点对称，若不是即可断定函数是非奇非偶函数．

2．利用函数的奇偶性补全函数的图象

(教材P₄₁思考题)

规律：

偶函数的图象关于y轴对称；

奇函数的图象关于原点对称．

　　　 说明：这也可以作为判断函数奇偶性的依据．

巩固练习：(教材P₄₂练习1)

3．函数的奇偶性与单调性的关系

(学生活动)举几个简单的奇函数和偶函数的例子，并画出其图象，根据图象判断奇函数和偶函数的单调性具有什么特殊的特征．

例3．已知f(x)是奇函数，在(0，+∞)上是增函数，证明：f(x)在(－∞，0)上也是增函数

解：(由一名学生板演，然后师生共同评析，规范格式与步骤)

规律：

偶函数在关于原点对称的区间上单调性相反；

奇函数在关于原点对称的区间上单调性一致．