2．　 尝试解决本小节开始提出的问题．

1．　 (对数的起源)价绍对数产生的历史背景与概念的形成过程，体会引入对数的必要性；

设计意图：激发学生学习对数的兴趣，培养对数学习的科学研究精神．

2．　 选做题：教材P₇₀习题2．1(B组) 第1题．

1．　 必做题：教材P₆₉习题2．1(A组) 第5、6、8、12题．

本节主要学习了指数函数的图象，及利用图象研究函数性质的方法．

(三)典型例题

例1．(教材P₆₆例6)．

解：(略)

问题：你能根据本例说出确定一个指数函数需要几个条件吗？

例2．(教材P₆₆例7)

解：(略)

问题：你能根据本例说明怎样利用指数函数的性质判断两个幂的大小？

说明：规范利用指数函数的性质判断两个幂的大小方法、步骤与格式．

巩固练习：(教材P₆₉习题A组第7题)

(二)指数函数的图象和性质

问题：你能类比前面讨论函数性质时的思路，提出研究指数函数性质的内容和方法吗？

研究方法：画出函数的图象，结合图象研究函数的性质．

研究内容：定义域、值域、特殊点、单调性、最大(小)值、奇偶性．

探索研究：

1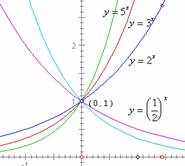．在同一坐标系中画出下列函数的图象：

(1)

(2)

(3)

(4)

(5)

2．从画出的图象中你能发现函数的图象和函数的图象有什么关系？可否利用的图象画出的图象？

3．从画出的图象(、和)中，你能发现函数的图象与其底数之间有什么样的规律？

4．你能根据指数函数的图象的特征归纳出指数函数的性质吗？

图象特征	函数性质
向x、y轴正负方向无限延伸	函数的定义域为R
图象关于原点和y轴不对称	非奇非偶函数
函数图象都在x轴上方	函数的值域为R+
函数图象都过定点(0，1)
自左向右看， 图象逐渐上升	自左向右看， 图象逐渐下降	增函数	减函数
在第一象限内的图象纵坐标都大于1	在第一象限内的图象纵坐标都小于1
在第二象限内的图象纵坐标都小于1	在第二象限内的图象纵坐标都大于1
图象上升趋势是越来越陡	图象上升趋势是越来越缓	函数值开始增长较慢，到了某一值后增长速度极快；	函数值开始减小极快，到了某一值后减小速度较慢；

5．　 利用函数的单调性，结合图象还可以看出： (1)在[a，b]上，值域是或； (2)若，则；取遍所有正数当且仅当； (3)对于指数函数，总有； (4)当时，若，则；

(一)指数函数的概念

　　　 一般地，函数叫做指数函数(exponential function)，其中x是自变量，函数的定义域为R．

　　　 注意：1 指数函数的定义是一个形式定义，要引导学生辨析；

2 注意指数函数的底数的取值范围，引导学生分析底数为什么不能是负数、零和1．

巩固练习：利用指数函数的定义解决(教材P₆₈例2、3)

4．　 上面的几个函数有什么共同特征？

3．　 一种放射性物质不断变化成其他物质，每经过一年的残留量是原来的84%，那么以时间x年为自变量，残留量y的函数关系式是什么？