1. 已知，则下列不等式一定成立的是(　　 )

A. 　　　B. 　　　C. 　　　D.

22．(本小题满分14分)已知中心在原点，焦点在轴上的椭圆C的离心率与双曲线的离心率互为倒数，且经过点，过点P(2，1)的直线与椭圆C在第一象限相切于点M .

　 (1)求椭圆C的方程；

　 (2)求直线的方程以及点M的坐标；

　 (3)是否存过点P的直线与椭圆C相交于不同的两点A、B，满足？若存在，求出直线l₁的方程；若不存在，请说明理由.

解：(1)设椭圆C的方程为，

双曲线的离心率为2，椭圆C的离心率……………1分

又据题意得　　　　　　　　　　　　　 …………………2分

解得，故椭圆C的方程为.……………………4分

(2)因为过点P(2，1)的直线l与椭圆在第一象限相切，所以l的斜率存在，故可设直线l的方程为…………………5分

由　　　 得. ①

……………………7分

因为直线与椭圆相切，所以

　　　　　　 整理，得　　　　　　　　　 解得

所以直线方程为　　　　　 …………………8分

将代入①式，可以解得M点横坐标为1，故切点M坐标为…………9分

　 (3)若存在直线l₁满足条件，的方程为，代入椭圆C的方程得

因为直线l₁与椭圆C相交于不同的两点A，B，设A，B两点的坐标分别为

所以

所以.　　　　　　　　　　　　　 ……………………10分

又，……………………11分

因为即，

……………………12分

所以.

　　　 即

　　　 所以，

解得　　　　　　　　　　　　　　　　　 ……………………13分

　　 因为A，B为不同的两点，所以.

　　　 于是存在直线₁满足条件，其方程为………………………………14分

21.(本小题满分12分) 设函数.

(1)若函数图象上的点(1,2)处的切线斜率为4，请判断函数的单调性；

　(2)已知当时，函数在上单调递增，求实数的取值范围.

解：(1)…………………………………1分

，， …………………………………3分

，…………………………………4分

恒成立，……………………………6分

(2)当时，，………………………7分

函数在上单调递增

在上恒成立，即在上恒成立，

…………………………………9分

，………………11分

　　　　　　　　　　　　　　　　 …………………………………12分

20．(本小题满分12分)已知数列中，其前项和满足

计算猜想的表达式，并用数学归纳法加以证明．

解：当时，　　　 …………1分

　 …………2分

则有：　　　 …………3分

……………………………………6分

用数学归纳法证明：

(1)　　　 当时，，成立…………………7分

(2)假设猜想成立，即成立…………………8分

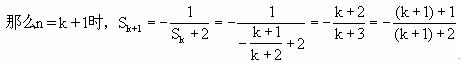
　　　　　　　　　　　　　　　　　　　　　　　　　 ………………10分

即n=k+1时猜想成立　　　　　　 ……………………………………11分

由(1)、(2)可知，对任意自然数n，猜想结论均成立．………………………12分

19.(本小题满分12分) 为考察某种药物预防疾病的效果，进行动物试验，调查了105个样本，统计结果为：服药的共有55个样本，服药但患病的仍有10个样本，没有服药且未患病的有30个样本.

(1)根据所给样本数据完成2×2列联表中的数据；

(2)请问能有多大把握认为药物有效？

(参考公式：独立性检验临界值表

概率	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

)

解：(1)依题得服药但没患病的共有45个样本，没有服药且患病的有20个样本，故可以得到以下2×2列联表：

……………………………………6分

(2)假设服药与患病没有关系，则的观测值应该很小，

而＝

　　　　　　　　　　　　　 …………………………………………………9分

∵6.109>5.024，

由独立性检验临界值表可以得出能有97.5%把握认为药物有效。　　 ………………12分

18．(本小题满分12分)已知复数在复平面上对应的点为．

(1)设集合，从集合中随机取一个数作为，从集合中随机取一个数作为，求复数为纯虚数的概率；

(2)设，求点落在不等式组：所表示的平面区域内的概率．

解：(1)记 “复数为纯虚数”为事件，

∵组成复数的所有情况共有12个：

，， ，，……………………2分

且每种情况出现的可能性相等，属于古典概型，其中事件包含的基本事件共2个: 　

……………………4分

∴所求事件的概率为 　　　　　　…………………………………………6分

(2)依条件可知，点均匀地分布在平面区域内，属于几何概型.

该平面区域的图形为右图中矩形围成的区域, 面积为

……………………8分

所求事件构成的平面区域为,其图形如下图中的三角形(阴影部分)，　　　　　　　　　　　　　　　 ……………………9分

又直线与轴、轴的交点分别为,

所以三角形的面积为……………………11分

∴所求事件的概率为　　 …………………12分

17．(本小题满分12分)

已知集合；命题，

命题，并且命题是命题的充分条件，求实数的取值范围．

解：先化简集合A，由，配方得：

　 …………………………………………………2分

　 …………………………………4分

化简集合B， 由或得或

…………………………………………………6分

，……………………………8分

……………………………………………………………10分

解之得………………………………………………11分

所以实数m的取值范围是或………………………12分

16.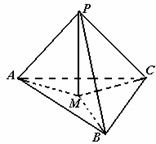 如图，在三棱锥P-ABC中，PA、PB、PC两两垂直，且PA=3，PB=2，PC=1，设M是底面ABC内一点，定义其中m,n,p分别是三棱锥M-PAB, 三棱锥M-PBC, 三棱锥M-PCA的体积，若且恒成立，则正实数a的最小值为　　 1　　　　 。

15．不等式对任意实数恒成立，则实数

的取值范围为　　 　　　　　　　　　

14．若执行如右图所示的程序框图，则输出的= 420　　　 .