
右图为我国某区域图,读图回答1--2题。
1.有关该区域特征说法错误的是
A.河流流量主要随气温变化而变化
B.河流M有凌汛现象
C.粮食商品率高,人均耕地面积大
D.实木家具城R接近原料产地
2.N地退耕还沼的主要目的是
A.可进一步提供大量粮食
B.提供更多的旅游欣赏景观
C.为农业生产提供充沛灌溉水源
 D.为区域可持续发展提供生态保障
D.为区域可持续发展提供生态保障
22.解:(1)n=1时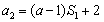
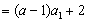
 ,
,
∴
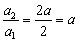 (常数).
(常数).
n≥2时,由已知an+1=(a-1)Sn+2有an=(a-1)Sn-1+2,
两式相减得an+1-an=(a-1)an,
整理得an+1=a·an,即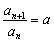 (常数)
(常数)
即对n=1,2,3,…,2k-1均有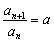 (常数)
(常数)
故{an}是以a1=2,a为公比的等比数列.
∴ an=2an-1.……………………………………………………………………5分
(2)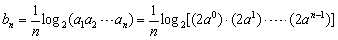


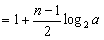 .……………………………………………………9分
.……………………………………………………9分
(3)由已知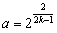 ,得
,得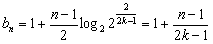 ,
,
由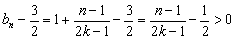 知
知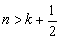 ,
,
∴
当n=1,2,…,k时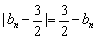 ,
,
当n=k+1,k+2,…,2k时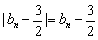 ,
,
∴

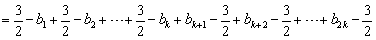
=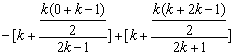
=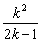 ,
,
∴
原不等式变为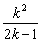 ≤4,解得
≤4,解得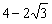 ≤k≤
≤k≤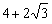 ,
,
∵ k∈N*,且k≥2,
∴ k=2,3,4,5,6,7.……………………………………………………14分
21.解:(1)∵ a=1时,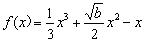 ,
,
∴
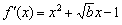 .
.
由题知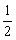 是方程
是方程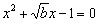 的根,代入解得
的根,代入解得 ,
,
于是 .
.
由 即
即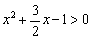 ,可解得x<-2,或x>
,可解得x<-2,或x>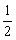 ,
,
∴
f (x)的单调递增区间是(-∞,-2),(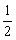 ,+∞).…………………………4分
,+∞).…………………………4分
(2)∵ 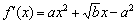 ,
,
∴
由题知x1,x2是方程ax2+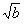 x-a2=0的两个根.
x-a2=0的两个根.
∴
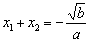 ,x1x2=-a,
,x1x2=-a,
∴ |x1-x2|=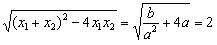 .
.
整理得b=4a2-4a3.……………………………………………………………8分
∵ b≥0,
∴ 0<a≤1.
则b关于a的函数g(a)=4a2-4a3(0<a≤1).
于是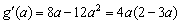 ,
,
∴
当 时,
时,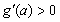 ;当
;当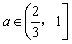 时,
时,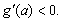
∴ g(a)在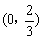 上是增函数,在
上是增函数,在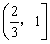 上是减函数.
上是减函数.
∴
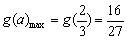 ,
,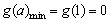 ,
,
∴ 0≤b≤ . ………………………………………………………………12分
. ………………………………………………………………12分
20.解:(1)令y=f (x)=ax+2-1,于是y+1=ax+2,
∴ x+2=loga(y+1),即x=loga(y+1)-2,
∴
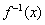 =loga(x+1)-2(x>-1).………………………………………………3分
=loga(x+1)-2(x>-1).………………………………………………3分
(2)当0<a<1时,
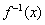 max=loga(0+1)-2=-2,
max=loga(0+1)-2=-2,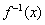 min=loga(1+1)-2=loga2-2,
min=loga(1+1)-2=loga2-2,
∴ -2-( -2)=2,解得
-2)=2,解得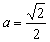 或
或 (舍).
(舍).
当a>1时,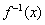 max=loga2-2,
max=loga2-2,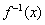 min=-2,
min=-2,
∴
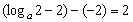 ,解得
,解得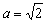 或
或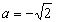 (舍).
(舍).
∴
综上所述,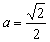 或
或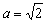 .……………………………………………7分
.……………………………………………7分
(3)由已知有loga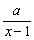 ≤loga(x+1)-2,
≤loga(x+1)-2,
即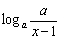 ≤
≤ 对任意的
对任意的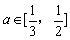 恒成立.
恒成立.
∵
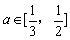 ,
,
∴
 ≤
≤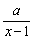 .①
.①
由 >0且
>0且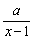 >0知x+1>0且x-1>0,即x>1,
>0知x+1>0且x-1>0,即x>1,
于是①式可变形为x2-1≤a3,
即等价于不等式x2≤a3+1对任意的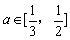 恒成立.
恒成立.
∵
u=a3+1在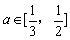 上是增函数,
上是增函数,
∴
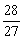 ≤a3+1≤
≤a3+1≤ ,于是x2≤
,于是x2≤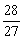 ,
,
解得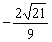 ≤x≤
≤x≤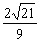 .
.
结合x>1得1<x≤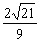 .
.
∴
满足条件的x的取值范围为 .…………………………………12分
.…………………………………12分
19.解:(1)设{an}的公差为d,由题设有
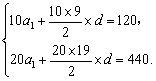 解得a1=3,d=2.……………………………………5分
解得a1=3,d=2.……………………………………5分
an=a1+(n-1)d=3+(n-1)×2=2n+1,
即{an}的通项公式为an=2n+1. ………………………………………………6分
(2)由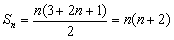 ,得
,得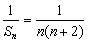 , ……………………8分
, ……………………8分
∴
Tn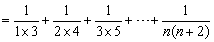

 ,
,
= . …………………………………………………12分
. …………………………………………………12分
18.解:(1)∵ A班的5名学生的平均得分为(5+9+9+9+9)÷5=8,
方差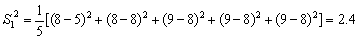 ;
;
B班的5名学生的平均得分为(6+7+8+9+10)÷5=8,
方差 .
.
∴ S12>S22,
∴ B班的预防知识的问卷得分要稳定一些.…………………………………8分
(2)共有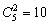 种抽取样本的方法,
种抽取样本的方法,
其中样本6和7,6和8,8和10,9和10的平均数满足条件,
故所求的概率为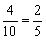 .………………………………………………………12分
.………………………………………………………12分
17.解:由 解得
解得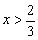 且x≠1,即A={x|
且x≠1,即A={x|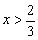 且x≠1},
且x≠1},
由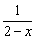 ≥1解得1≤x<2,即B={x|1≤x<2}.
………………………………4分
≥1解得1≤x<2,即B={x|1≤x<2}.
………………………………4分
(1)于是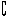 RA={x|x≤
RA={x|x≤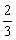 或x=1},所以(
或x=1},所以(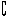 RA)∩B={1}. ……………………7分
RA)∩B={1}. ……………………7分
(2)∵ A∪B={x|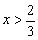 },即C={x|
},即C={x|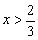 }.
}.
由|x-a|<4得a-4<x<a+4,即M={x|a-4<x<a+4}.
∵ M∩C=Æ,
∴
a+4≤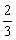 ,解得a≤
,解得a≤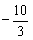 .…………………………………………………12分
.…………………………………………………12分
13.0 14.500 15.a=-1(答案不唯一)16.②⑤
BCCAD DABAC DB
22.(本题满分14分)已知数列{an}共有2k项(k∈N*,k≥2),首项a1=2.设{an}的前n项的和为Sn,且an+1=(a-1)Sn+2(n=1,2,3,…,2k-1),其中常数a>1.
(1)求证{an}是等比数列,并求{an}的通项公式;
(2)若数列{bn}满足 (n=1,2,3,…,2k),求{bn}的通项公式;
(n=1,2,3,…,2k),求{bn}的通项公式;
(3)令a=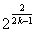 ,对(2)中的{bn}满足不等式
,对(2)中的{bn}满足不等式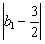 +
+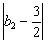 +…+
+…+ +
+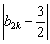 ≤4,求k的值.
≤4,求k的值.
绵阳市高中2010届高三第一次诊断性考试
数学(文)参考解答及评分标准
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com