
1.已知M={x|x2>4},N={x|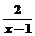 ≥1},则CRM∩N=( )
≥1},则CRM∩N=( )
A. {x|1<x≤2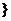 B.{x|-2≤x≤1} C. {x|1≤x≤.2
B.{x|-2≤x≤1} C. {x|1≤x≤.2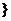 D.{x|x<2}
D.{x|x<2}
21.(本小题满分14分)
解法一:(Ⅰ)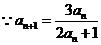 ,
,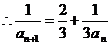 ,
,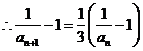 ,
……………………2分
,
……………………2分
又 ,
,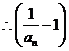 是以
是以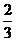 为首项,
为首项,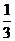 为公比的等比数列. ………3分
为公比的等比数列. ………3分
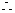
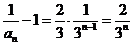 ,
,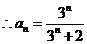 .
……………………4分
.
……………………4分
(Ⅱ)由(Ⅰ)知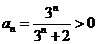 ,
……………………5分
,
……………………5分
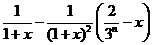
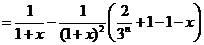
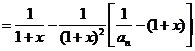
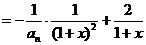
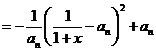
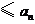 ,
, 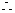 原不等式成立.………………8分
原不等式成立.………………8分
(Ⅲ)由(Ⅱ)知,对任意的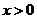 ,有
,有
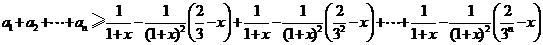
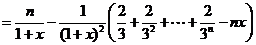 . ……………………10分
. ……………………10分
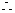 取
取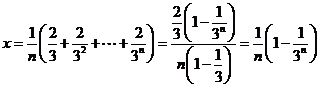 ,…………12分
,…………12分
则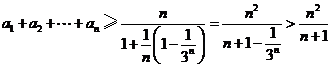 .
.
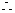 原不等式成立.
……………………14分
原不等式成立.
……………………14分
解法二:(Ⅰ)同解法一.
(Ⅱ)设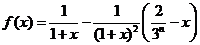 , ……………………5分
, ……………………5分
则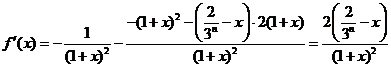 …………6分
…………6分
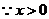 ,
,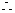 当
当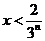 时,
时,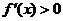 ;当
;当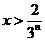 时,
时,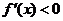 ,
,
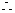 当
当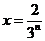 时,
时,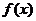 取得最大值
取得最大值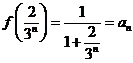 .
.
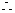 原不等式成立.
……………………8分
原不等式成立.
……………………8分
(Ⅲ)同解法一.
20.(本小题满分14分)
解:(Ⅰ)由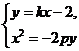 得,
得,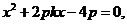 ……………………2分
……………………2分
设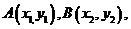 则
则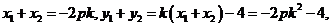
因为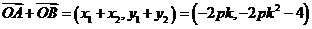 =
=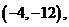
所以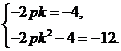 解得
解得 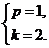 ………………4分
………………4分
所以直线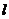 的方程为
的方程为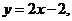 抛物线C的方程为
抛物线C的方程为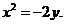 …………6分
…………6分
(Ⅱ)方法1:设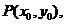 依题意,抛物线过P的切线与
依题意,抛物线过P的切线与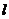 平行时,△APB面积最大,
平行时,△APB面积最大,
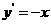 ,所以
,所以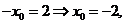
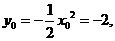 所以
所以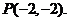
此时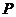 到直线
到直线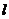 的距离
的距离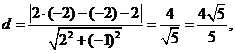 ………………8分
………………8分
由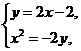 得,
得,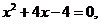 ………………………10分
………………………10分
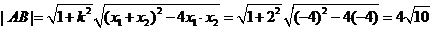
∴△ABP的面积最大值为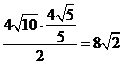 。 …………………………14分
。 …………………………14分
(Ⅱ)方法2:由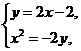 得,
得,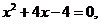 ……………………8分
……………………8分
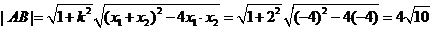 ……9分
……9分
设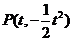 ,
,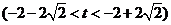
因为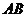 为定值,当
为定值,当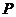 到直线
到直线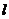 的距离
的距离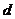 最大时,△ABP的面积最大,
最大时,△ABP的面积最大,
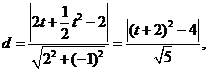 ……………………………12分
……………………………12分
因为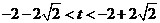 ,所以当
,所以当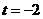 时,
时,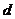 max=
max=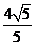 ,此时
,此时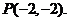
∴△ABP的面积最大值为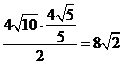 。……………………………14分
。……………………………14分
19.(本小题满分14分)
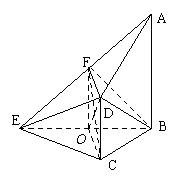 解法1:(Ⅰ)证明:取BE的中点O,连OC,OF,DF,则2OF
解法1:(Ⅰ)证明:取BE的中点O,连OC,OF,DF,则2OF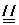 BA ………………2分
BA ………………2分
∵AB⊥平面BCE,CD⊥平面BCE,∴2CD 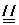 BA,
BA,
∴OF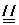 CD,∴OC∥FD ………………4分
CD,∴OC∥FD ………………4分
∵BC=CE,∴OC⊥BE,又AB⊥平面BCE.
∴OC⊥平面ABE. ∴FD⊥平面ABE.
从而平面ADE⊥平面ABE. ………………6分
(Ⅱ)二面角A-EB-D与二面角F-EB-D相等,由(Ⅰ)知二面角F-EB-D的平面角为∠FOD。BC=CE=2, ∠BCE=1200,OC⊥BE得BO=OE=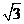 ,OC=1,∴OFDC为正方形,∴∠FOD=450,
,OC=1,∴OFDC为正方形,∴∠FOD=450,
∴二面角A-EB-D的余弦值为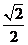 。 ……………………10分
。 ……………………10分
(Ⅲ)∵OFDC为正方形,∴CF⊥OD,CF⊥EB,∴CF⊥面EBD,
∴点F到平面BDE的距离为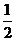 FC,∴点F到平面BDE的距离为
FC,∴点F到平面BDE的距离为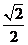 。……………14分
。……………14分
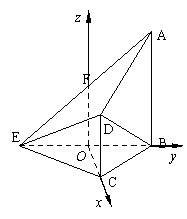
解法2:取BE的中点O,连OC.∵BC=CE, ∴OC⊥BE,又AB⊥平面BCE.
以O为原点建立如图空间直角坐标系O-xyz,
则由已知条件有: 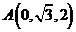 ,
,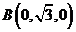 ,
,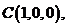
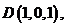

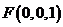 ……………………………2分
……………………………2分
设平面ADE的法向量为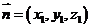 ,
,
则由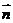 ·
·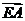
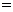
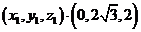
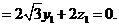
及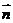 ·
·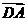
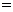
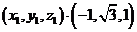
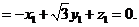
可取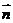
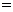
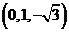 …………………………… 4分
…………………………… 4分
又AB⊥平面BCE,∴AB⊥OC,OC⊥平面ABE,
∴平面ABE的法向量可取为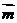 =
=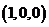 .
.
∵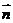 ·
·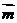
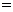
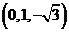 ·
·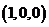 =0,
∴
=0,
∴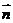 ⊥
⊥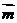 ,∴平面ADE⊥平面ABE.…… 6分
,∴平面ADE⊥平面ABE.…… 6分
(Ⅱ)设平面BDE的法向量为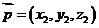 ,
,
则由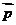 ·
·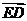
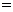
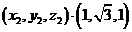
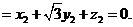
及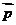 ·
·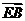
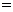
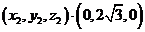
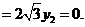 可取
可取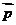
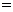
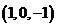 ……… 7分
……… 7分
∵平面ABE的法向量可取为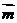 =
=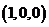 …………8分
…………8分
∴锐二面角A-EB-D的余弦值为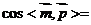
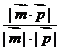 =
=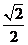 ,………… 9分
,………… 9分
∴二面角A-EB-D的余弦值为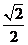 。
……………………………10分
。
……………………………10分
(Ⅲ)点F到平面BDE的距离为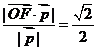 。……………………………14分
。……………………………14分
18.(本小题满分12分)
解:(Ⅰ)∵函数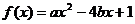 的图象的对称轴为
的图象的对称轴为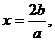
要使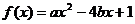 在区间
在区间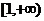 上为增函数,
上为增函数,
当且仅当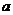 >0且
>0且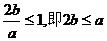 …………………………………………2分
…………………………………………2分
若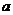 =1则
=1则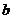 =-1,
=-1,
若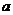 =2则
=2则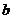 =-1,1
=-1,1
若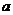 =3则
=3则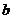 =-1,1;
…………………………………………4分
=-1,1;
…………………………………………4分
∴事件包含基本事件的个数是1+2+2=5
∴所求事件的概率为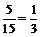 …………………………………………6分
…………………………………………6分
(Ⅱ)由(Ⅰ)知当且仅当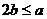 且
且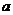 >0时,
>0时,
函数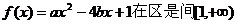 上为增函数,
上为增函数,
依条件可知试验的全部结果所构成的区域为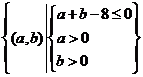
构成所求事件的区域为三角形部分。 …………………………………………8分
由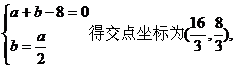 …………………………………………10分
…………………………………………10分
∴所求事件的概率为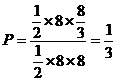 …………………………………………12分
…………………………………………12分
17.(本小题满分14分)
解:(I)当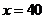 时,汽车从甲地到乙地行驶了
时,汽车从甲地到乙地行驶了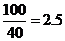 小时, ………………2分
小时, ………………2分
要耗油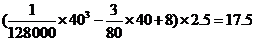 (升)。 ………………4分
(升)。 ………………4分
答:当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地耗油17.5升。…6分
(II)当速度为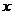 千米/小时时,汽车从甲地到乙地行驶了
千米/小时时,汽车从甲地到乙地行驶了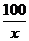 小时,设耗油量为
小时,设耗油量为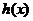 升,
升,
依题意得
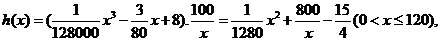 ………8分
………8分
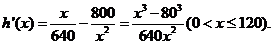 令
令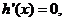 得
得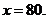 ……10分
……10分
当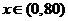 时,
时,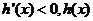 是减函数; 当
是减函数; 当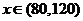 时,
时,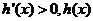 是增函数。
是增函数。
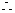 当
当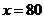 时,
时,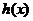 取到极小值
取到极小值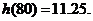 …………………………12分
…………………………12分
因为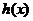 在
在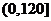 上只有一个极值,所以它是最小值。
上只有一个极值,所以它是最小值。
答:当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少为11.25升。14分
16.(本小题满分12分)
解:(Ⅰ)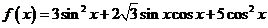
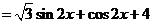
=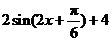 .…………………………………………………… 3分
.…………………………………………………… 3分
∴周期为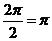 , …………………………………………………… 4分
, …………………………………………………… 4分
最大值为6 …………………………………………………………………… 5分
(Ⅱ)由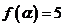 ,得
,得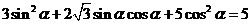 .………………… 6分
.………………… 6分
∴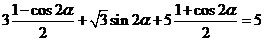 . …………………………… 7分
. …………………………… 7分
∴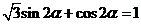 , ………………………………………………… 8分
, ………………………………………………… 8分
即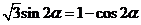
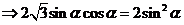 ………… 9分
………… 9分
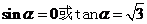 , ………………………………………………………10分
, ………………………………………………………10分
∴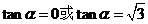 . …………………………………………………… 12分
. …………………………………………………… 12分
15、解析:连结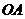 ,则
,则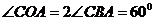 ,且由
,且由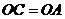 知
知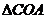 为正三角形,所以
为正三角形,所以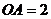 。又因为
。又因为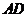 是⊙
是⊙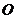 的切线,即
的切线,即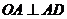 ,所以
,所以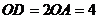
14、解析: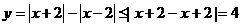
13、解析:在平面直角坐标系中,曲线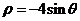 和
和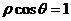 分别表示圆
分别表示圆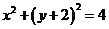 和直线
和直线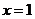 ,作图易知
,作图易知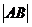 =
=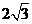 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com